Question

已知集合A={x|},B={x||x-3|＜a},若A∪B=A,求实数a的取值范围.

Answer 1

思路解析：分别化简集合A和B,在化简集合B时,要注意对字母a的讨论.化简之后根据已知条件A∪B=A知BA.然后转化,把题意转化为关于a的不等式,从而求出a的取值范围.

解：对A,由知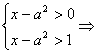x＞a²+1,

所以A={x|x＞a²+1},

由A∪B=A知BA.

对B,当a≤0时,B=符合题意.(*)

当a＞0时,B={x|3-a＜x＜3+a}.

而BA,所以a²+1≤3-a,

解之得-2≤a≤1,∴0＜a≤1.

综合(*)得,满足题意的a的取值范围是a≤1.