Question

若方程x=-b+

1-(x-1)2

恰有一个实根，则b的取值范围为（　　）

• A、-2≤b≤0
• B、-1-

  2

  ≤b≤-1+

  2

• C、-2≤b＜0或b=-1+

  2

• D、0＜b≤-1+

  2

Answer 1

分析：依题意，x+b=

1-(x-1)2

，构造函数y=x+b与y=

1-(x-1)2

，在同一坐标系里作出它们的图象即可求得答案．

解答：解：∵x=-b+

1-(x-1)2

，
∴x+b=

1-(x-1)2

，
令y=x+b与y=

1-(x-1)2

，在同一坐标系里作出它们的图象如下：

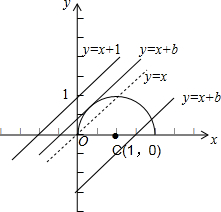
由图知，当直线y=x+b与方程为y=

1-(x-1)2

的上半圆相切或从直线y=x开始向右平移与该半圆相交时，两曲线只有一个交点，即方程x=-b+

1-(x-1)2

只有一个实数根．
当直线y=x+b与方程为y=

1-(x-1)2

的上半圆相切时，圆心C（1，0）到直线y=x+b的距离d=

|1-0+b|

12+12

=

|1+b|

2

=1（b＞0），
解得b=

2

-1；
当直线y=x+b从直线y=x开始（不包括直线y=x）向右平移与该半圆相交时，两曲线只有一个交点，y=x+b经过（2，0）时，b达到最小值-2，
∴-2≤b＜0；
综上所述，b=

2

-1或-2≤b＜0．
故选：C．

点评：本题考查函数的零点，着重考查直线与圆的位置关系，突出考查点到直线间的距离，考查转化思想、数形结合思想、分类讨论思想的综合应用，考查作图能力，属于中档题．