题目内容

1．已知tan（α-β）=2，tan（α+β）=7，求tan2β的值．

分析 根据2β=（α+β）-（α-β），利用两角差的正切公式即可求出结论．

解答 解：∵tan（α-β）=2，tan（α+β）=7，
∴tan2β=tan[（α+β）-（α-β）]
=$\frac{tan（α+β）-tan（α-β）}{1+tan（α+β）tan（α-β）}$
=$\frac{7-2}{1+7×2}$
=$\frac{1}{3}$．

点评 本题考查了两角和与差的正切公式的应用问题，是基础题目．

练习册系列答案
相关题目
11．已知函数f（x）=|2x-a|+a，若不等式f（x）＜6的解集为（-1，3），求a的值．
12．若f（x）=（a-1）x2+ax+3是偶函数，则f（3）=-6．
9．以点（-1，4）为圆心，半径为3的圆的方程是（x+1）2+（y-4）2=9．
16．函数f（x）=2cos（ωx+θ）（x∈R，ω＞0，0≤θ≤$\frac{π}{2}$）的图象与x轴相交于点（$\frac{π}{6}$，0），且函数相邻两条对称轴的距离为$\frac{π}{2}$．
（1）求θ和ω的值；
（2）若f（$\frac{1}{2}$x+$\frac{π}{6}$）=$\frac{8}{5}$，x∈（-$\frac{π}{2}$，$\frac{π}{2}$），求$\frac{sin2x}{1+cos2x}$值．
6．如果实数x，y满足条$\left\{\begin{array}{l}{2x-y-1≥0}\\{2x+y-4≤0}\\{y-1≥0}\end{array}\right.$则z=$\frac{2x-y}{x}$的最大值为$\frac{4}{3}$．
13．已知数列{an}满足a1+2a2+3a3+…+nan=$\frac{{n}^{2}}{2}$-n
（1）求数列{an}的通项公式；
（2）数列{an}有没有最小项？若有，求出这个最小项；若没有，请说明理由．
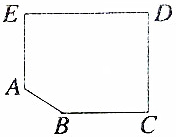10．某小区内有一块荒地ABCDE，今欲在该荒地上划出一块长方形地面（不改变方位）进行开发（如图所示），问如何设计才能使开发的面积最大？最大开发面积是多少？（已知BC=210m，CD=240m，DE=300m，EA=180m）
16．在同一坐标系中，直线l是函数f（x）=$\sqrt{1-{x}^{2}}$在（0，1）处的切线，若直线l也是g（x）=-x2+mx的切线，则m=±2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网