题目内容
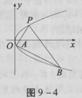
如图,过抛物线y2=2px(p>0)上一定点p(x0,y0)(y0>0),作两条直线分别交抛物线于A (x1,y1),B(x2,y2).
(1)求该抛物线上纵坐标为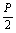 的点到其焦点F的距离;
的点到其焦点F的距离;
(Ⅱ)当PA与PB的斜率存在且倾斜角互补时, 求
求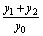 的值,并证明直线AB的斜率是非零常数.
的值,并证明直线AB的斜率是非零常数.
(1)当y= 时,x=
时,x= ,又抛物线y2= 2px的准线方程为x=
,又抛物线y2= 2px的准线方程为x= ,
,
由抛物线定义得,所求距离为 -(-
-(- )=
)=
(Ⅱ)设直线PA的斜率为kPA,直线PB的斜率为kPB
由y12=2px1,y20=2px0
相减得(y1-y0)(yl+y0)=2P(x1-x0),
故kPA= (x1≠x0).
(x1≠x0).
同理可得kPB= (x2≠x0).
(x2≠x0).
由PA、PB倾斜角互补知kPA=-kPB,
即 =-
=- ,所以yl+y2=-2y0,
,所以yl+y2=-2y0,
故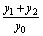 =-2. 设直线AB的斜率为kAB
=-2. 设直线AB的斜率为kAB
由y22=2px2,y21=2pxl
相减得(y2-y1)(y2+y1)=2p(x2-x1),
所以
将yl+y2 =-2y0(y0>0)代入得
=-2y0(y0>0)代入得
 所以kAB是非零常数.
所以kAB是非零常数.

练习册系列答案
相关题目
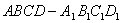 内盛有一半的水,密封后将底面
内盛有一半的水,密封后将底面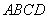 放在水平桌面上,然后将该长方体绕
放在水平桌面上,然后将该长方体绕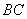 慢慢转动使之倾斜,在此过程中有下列四种说法
慢慢转动使之倾斜,在此过程中有下列四种说法 始终与水面平行;
始终与水面平行; 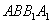 与水接触面的面积始终不变;
与水接触面的面积始终不变; 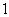 B.
B.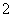 C.
C.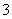 D.
D.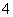
 的最小值是 ( )
的最小值是 ( )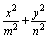 =1中的m和n,则能组成落在矩形区域B={(x,y)‖x|<11,且|y|<9}内的椭圆个数为 ( )
=1中的m和n,则能组成落在矩形区域B={(x,y)‖x|<11,且|y|<9}内的椭圆个数为 ( )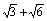 B.
B.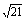 C.18+12
C.18+12 D.21
D.21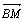 =λ
=λ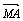 ,证明线段PM的中点在y轴上
,证明线段PM的中点在y轴上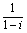 的共轭复数是 ( )
的共轭复数是 ( )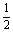 +
+