Question

【题目】已知函数（）

(1)若是的极值，求的值，并求的单调区间。

(2)若时，，求实数的取值范围。

Answer 1

【答案】（1），的单调减区间为，单调增区间为.（2）

【解析】

（1）计算的导函数，结合极值，计算a，结合导函数与原函数单调关系，计算单调区间，即可。（2）法一：计算导函数，构造函数，结合导函数，得到的单调区间，计算范围，即可。法二 ：构造函数，结合导函数，得到原函数单调性，计算，得到a的范围，即可。

(1)的定义域是，，

由是的极值得，得.

时，由，得，

列表（列表的功能有两个：一是检验的正确性；二是求单调区间）得

	负	0	正
	单调递减	极小值	单调递增

综上，，的单调减区间为，单调增区间为.

(2)法一：因，.

记，

则，且，当，

即时，，在单调递增，

故时，，则，

则在单调递增，，符合。

当，即时，则存在，使得时，，

此时，，在单调递减，时，，不符。

综上，实数的取值范围是.

法二：时，，等价于，

记，

则，

记，

则，

故，在单调递减，

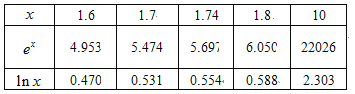
由洛必达法则得，

故，综上，实数的取值范围是.