题目内容
【题目】已知函数![]() ,
,![]() R.
R.
(1)试讨论函数![]() 的极值点的个数;
的极值点的个数;
(2)若![]() N*,且
N*,且![]() 恒成立,求
恒成立,求![]() 的最大值.
的最大值.
参考数据:
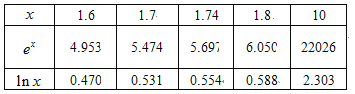
【答案】(1)见解析;(2)10
【解析】
(1)先求出函数的导数,通过讨论![]() 的范围,即可求出函数的单调区间;
的范围,即可求出函数的单调区间;
(2)先由(1)可确定![]() 时,
时,![]() 有唯一极大值点
有唯一极大值点![]() ,进而可表示出
,进而可表示出![]() 的最大值,因此
的最大值,因此![]() 恒成立即转化为
恒成立即转化为![]() 的问题,再构造函数
的问题,再构造函数![]() ,用导数的方法研究其单调性和最值即可得出结果.
,用导数的方法研究其单调性和最值即可得出结果.
(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() 。当
。当![]() 时,
时,![]() ,
,
![]() 在定义域
在定义域![]() 单调递减,
单调递减,![]() 没有极值点;
没有极值点;
②当![]() 时,
时,![]() 在
在![]() 单调递减且图像连续,
单调递减且图像连续,
![]() ,
,![]() 时
时![]() ,所以存在唯一正数
,所以存在唯一正数![]() ,使得
,使得![]() ,
,
函数![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,
所以函数![]() 有唯一极大值点
有唯一极大值点![]() ,没有极小值点
,没有极小值点
综上:当![]() 时,
时,![]() 没有极值点;
没有极值点;
当![]() 时,
时,![]() 有唯一极大值点,没有极小值点
有唯一极大值点,没有极小值点
(2)方法一:
由(1)知,当![]() 时,
时,![]() 有唯一极大值点
有唯一极大值点![]() ,所以
,所以![]() ,
,
![]() 恒成立
恒成立![]()
![]()
因为![]() ,所以
,所以![]() ,
,
所以![]() .
.
令![]() ,则
,则![]() 在
在![]() 单调递增,
单调递增,
由于![]() ,
,![]() ,
,
所以存在唯一正数![]() ,使得
,使得![]() ,
,
从而![]() .
.
由于![]() 恒成立,
恒成立,
①当![]() 时,
时,![]() 成立;
成立;
②当![]() 时,由于
时,由于![]() ,所以
,所以![]() .
.
令![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递减,从而
单调递减,从而![]() .
.
因为![]() ,且
,且![]() ,且
,且![]() N*,所以
N*,所以![]() .
.
下面证明![]() 时,
时,![]() .
.
![]() ,且
,且![]() 在
在![]() 单调递减,由于
单调递减,由于![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,
,
所以![]() .
.
令![]() ,
,![]() ,易知
,易知![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,
,
所以![]()
即![]() 时,
时,![]() .
.
所以![]() 的最大值是10.
的最大值是10.
方法二:
由于![]() 恒成立,所以
恒成立,所以
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
![]() ,
,![]() ;
;
因为![]() N*,所以猜想:
N*,所以猜想:![]() 的最大值是10.
的最大值是10.
下面证明![]() 时,
时,![]() .
.
![]() ,且
,且![]() 在
在![]() 单调递减,由于
单调递减,由于![]() ,
,
所以存在唯一![]() ,使得
,使得![]() ,
,
所以![]() .
.
令![]() ,
,![]() ,易知
,易知![]() 在
在![]() 单调递减,
单调递减,
所以![]() ,
,
所以![]()
即![]() 时,
时,![]() .
.
所以![]() 的最大值是10.
的最大值是10.

【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
【题目】某地区2007年至2011年农村居民家庭纯收入y(单位:千元)的数据如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 |
年份代号t | 1 | 2 | 3 | 4 | 5 |
人均纯收入y | 3.1 | 3.6 | 3.9 | 4.4 | 5 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2011年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: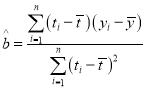 ,
,![]()