题目内容
12．
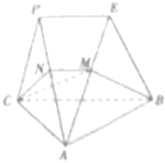如图，平面PAC⊥平面ABC，AC⊥BC，△PAC是等边三角形，PE∥BC，过BC作平面CNMB交线段AP于点N，交线段AE于M．（1）求证：MN∥PE；
（2）若平面ABC与平面MNC所成的锐二面角为30°，试确定点N的位置．
分析 （Ⅰ）由PE∥CB，得BC∥平面APE，由此能证明MN∥PE．
（Ⅱ）由MN∥BC，得C、B、M、N共面，∠NCA为二面角N-CB-A的平面角，由此确定点N的位置．
解答 （1）证明：因为PE∥CB，所以BC∥平面APE …（3分）
又依题意平面ABC交平面APE于MN，
故MN∥BC，
所以MN∥PE．…（6分）
（2）解：由（1）知MN∥BC，故C、B、M、N共面，
平面ABC与平面MNC所成的锐二面角即N-CB-A．
因为平面PAC⊥平面ABC，
平面PAC∩平面ABC=AC，且CB⊥AC，
所以CB⊥平面PAC．故CB⊥CN，
故∠NCA为二面角N-CB-A的平面角…（10分）
所以∠NCA=30°．
所以CN⊥PA．
所以N是PA的中点．…（14分）
点评 本题考查直线与直线平行的证明，考查使锐二面角的大小为30°的点N的位置，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
相关题目
17．
如果图中的程序执行后输出的结果是720，那么在程序While后面的条件应为（ ）
如果图中的程序执行后输出的结果是720，那么在程序While后面的条件应为（ ）| A． | i＞8 | B． | i＞7 | C． | i≥7 | D． | i≥6 |
现有四种不同颜色的染料，给如图的四个不同区域染色，每个区域只染一种颜色，相邻区域染不同的颜色，不同颜色可重复使用，则共有108种不同分染色方法（用数字作答）
1．下表给出一个等比数阵
其中每行每列都是等比数列，aij
表示第i行第j列的数．
（1）写出a34的值并求出aij的计算公式；
（2）若数列{bn}满足bn=a2n+log2a2n，求数列{bn}的前n项和Sn．
| 1 | 2 | （ ） | （ ） | （ ） | … | a1j | … |
| 3 | 6 | （ ） | （ ） | （ ） | … | a2j | … |
| （ ） | （ ） | （ ） | （ ） | （ ） | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| （ ） | （ ） | （ ） | （ ） | （ ） | … | … | … |
表示第i行第j列的数．
（1）写出a34的值并求出aij的计算公式；
（2）若数列{bn}满足bn=a2n+log2a2n，求数列{bn}的前n项和Sn．