题目内容
直线y=x与椭圆C: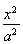 +
+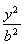 =1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
=1的交点在x轴上的射影恰好是椭圆的焦点,则椭圆C的离心率为( )
(A) 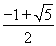 (B)
(B) 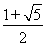
(C) 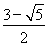 (D)
(D) 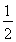
【答案】
A
【解析】设直线y=x与椭圆C: 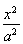 +
+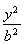 =1在第一象限的交点为A,依题意得点A的坐标为(c,c),
=1在第一象限的交点为A,依题意得点A的坐标为(c,c),
又点A在椭圆C上,故有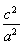 +
+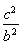 =1,
=1,
因为b2=a2-c2,
所以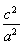 +
+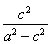 =1,
=1,
所以c4-3a2c2+a4=0,
即e4-3e2+1=0,
所以e=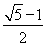 (e=
(e=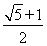 舍去).
舍去).
故选A.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
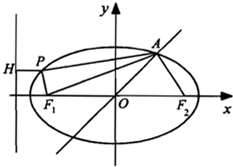 已知椭圆C:
已知椭圆C: 已知椭圆
已知椭圆