题目内容
函数 图象如图,则函数
图象如图,则函数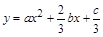 的单调递增区间为
的单调递增区间为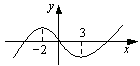
A.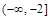 | B.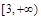 | C.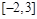 | D.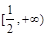 |
D
解析考点:利用导数研究函数的单调性.
分析:先对函数f(x)=x3+bx2+cx+d进行求导,根据x=-2,x=3时函数取到极值点知f’(-2)=0 f’(3)=0,故可求出bc的值,再根据函数单调性和导数正负的关系得到答案.
解答:解:∵f(x)=x3+bx2+cx+d,∴f’(x)=3x2+2bx+c
由图可知f’(-2)=0,f’(3)=0
∴12-4b+c=0,27+6b+c=0,∴b=-1.5,c=-18
∴y=x2-x-6,y’=2x-1,当x>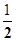 时,y’>0
时,y’>0
∴y=x2-x-6的单调递增区间为:[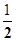 ,+∞)
,+∞)
故选D.
点评:本题主要考查函数极值点和单调性与函数的导数之间的关系.属基础题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
下列四个函数中,在区间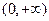 上单调递增的函数是 ( )
上单调递增的函数是 ( )
A.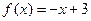 | B.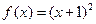 | C.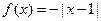 | D.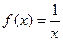 |
下列函数中,最小值为2的是( )
A. | B. |
C. | D. |
定义两种运算: ,
,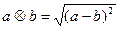 ,
,
则函数
| A.是奇函数 | B.是偶函数 |
| C.既是奇函数又是偶函数 | D.既不是奇函数又不是偶函数 |
函数y=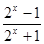 是( )
是( )
| A.奇函数 | B.偶函数 | C.非奇非偶函数 | D.既是奇函数又是偶函数 |
定义在R上的函数 ,当
,当 时,
时, ,且满足下列条件:
,且满足下列条件:
① ②
② , ③
, ③ .则
.则 等于
等于
A. | B. | C. | D. |
函数 在
在 上的最小值是
上的最小值是
| A.0 | B.1 | C.2 | D.3 |
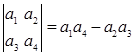 ,将函数
,将函数 的图像向左平移
的图像向左平移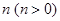 个单位,所得图像对应的函数为偶函数,则
个单位,所得图像对应的函数为偶函数,则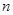 的最小值为 ( )
的最小值为 ( )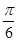
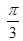
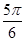
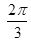
 ,
, ,给出四个图形,其中以集合
,给出四个图形,其中以集合 为定义域,
为定义域, 为值域的函数关系的是( )
为值域的函数关系的是( )