题目内容
定义式子运算为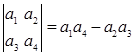 ,将函数
,将函数 的图像向左平移
的图像向左平移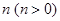 个单位,所得图像对应的函数为偶函数,则
个单位,所得图像对应的函数为偶函数,则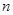 的最小值为 ( )
的最小值为 ( )
A.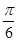 | B.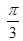 | C.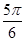 | D.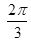 |
C
解析考点:函数y=Asin(ωx+φ)的图象变换;二阶矩阵.
专题:计算题.
分析:先根据题意确定函数f(x)的解析式,然后根据左加右减的原则得到平移后的解析式,再根据偶函数的性质可确定n的值.
解答:解:由题意可知f(x)=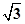 cosx-sinx=2cos(x+
cosx-sinx=2cos(x+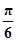 )
)
将函数f(x)的图象向左平移n(n>0)个单位后得到y=2cos(x+n+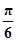 )为偶函数
)为偶函数
∴2cos(-x+n+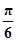 )=2cos(x+n+
)=2cos(x+n+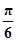 )
)
∴cosxcos(n+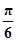 )+sinxsin(n+
)+sinxsin(n+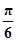 )=cosxcos(n+
)=cosxcos(n+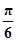 )-sinxsin(n+
)-sinxsin(n+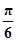 )
)
∴sinxsin(n+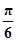 )=-sinxsin(n+
)=-sinxsin(n+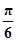 )
)
∴sinxsin(n+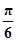 )=0∴sin(n+
)=0∴sin(n+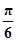 )=0∴n+
)=0∴n+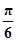 =kπ
=kπ
∴n=-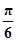 +kπ
+kπ
n大于0的最小值等于
故选C.
点评:本题主要考查两角和与差的余弦公式、三角函数的奇偶性和平移变换.平移时根据左加右减上加下减的原则进行平移.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知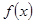 是R上的偶函数,且在区间
是R上的偶函数,且在区间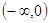 上是增函数,若
上是增函数,若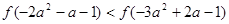 ,那么实数
,那么实数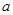 的取值范围是( )
的取值范围是( )
| A.(-1,0) | B.(-∞,0)∪(3,+∞) | C.(3,+∞) | D.(0,3) |
函数 图象如图,则函数
图象如图,则函数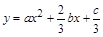 的单调递增区间为
的单调递增区间为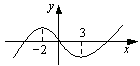
A.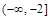 | B.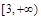 | C.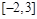 | D.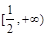 |
在下列函数中,既是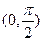 上的增函数,又是以
上的增函数,又是以 为最小正周期的偶函数的是( )
为最小正周期的偶函数的是( )
A. | B.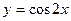 | C. | D. |
设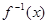 是函数
是函数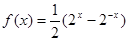 的反函数,则使
的反函数,则使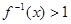 成立的x的取值范围为 ( )
成立的x的取值范围为 ( )
A.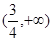 | B.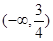 | C.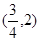 | D.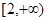 |
给出下列三个函数图像:

它们对应的函数表达式分别满足下列性质中的至少一条:
①对任意实数
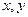 都有
都有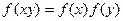 成立; ②对任意实数
成立; ②对任意实数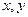 都有
都有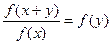 成立;
成立;③对任意实数
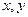 都有
都有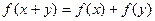 成立. 则下列对应关系最恰当的是
成立. 则下列对应关系最恰当的是 A. 和①, 和①,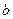 和②,c和③ 和②,c和③ | B.c和①,b和②, 和③ 和③ |
C.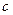 和①, 和①, 和②, 和②,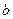 和③ 和③ | D.b和①,c和②, 和③ 和③ |
定义运算: 已知函数
已知函数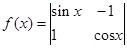 ,则函数
,则函数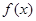 的最小正周期是
的最小正周期是
A.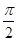 | B.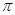 | C.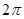 | D.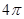 |
若函数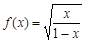 的定义域为A,函数
的定义域为A,函数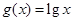 ,
,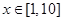 的值域为B,则A
的值域为B,则A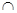 B为
B为
A.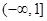 | B.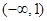 | C.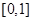 | D.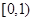 |