题目内容
(Ⅰ)在平面直角坐标系中,已知某点P(x,y),直线l:Ax+By+C=0.求证:点P到直线l的距离 .
.(Ⅱ)已知抛物线C:y2=4x的焦点为F,点P(2,0),O为坐标原点,过P的直线l与抛物线C相交于A,B两点,若向量
 在向量
在向量 上的投影为n,且
上的投影为n,且 ,求直线l的方程.
,求直线l的方程.
【答案】分析:(Ⅰ)分类讨论,利用构造直角三角形的方法,可以证明结论成立;
(Ⅱ)当直线l⊥x轴时,与已知矛盾,设直线方程代入抛物线方程,利用韦达定理,借助于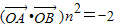 ,可得直线的斜率,从而可得直线l的方程.
,可得直线的斜率,从而可得直线l的方程.
解答:(Ⅰ)证明:当A=0,B≠0时,直线l:y=-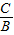 ,点P到直线l的距离d=|
,点P到直线l的距离d=|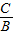 +y|;
+y|;
当A≠0,B=0时,直线l:x=-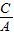 ,点P到直线l的距离d=|
,点P到直线l的距离d=|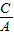 +x|
+x|
当AB≠0时,如图,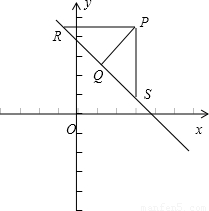 则R(
则R(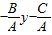 ,y),S(
,y),S(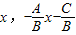 )
)
∴PR=|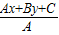 |,PS=|
|,PS=|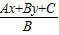 |
|
PQ是直角△PRS斜边上的高,由三角形面积公式可得PQ=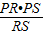 =
=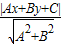
综上知,点P到直线l的距离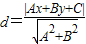 .
.
(Ⅱ)解:当直线l⊥x轴时,与已知矛盾;
故可设直线方程:y=k(x-2),A(x1,y1),B(x2,y2)
∴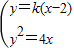 ,∴ky2-4y-8k=0
,∴ky2-4y-8k=0
∴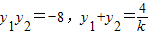 .
.
代入抛物线方程可得: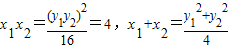
∵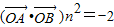 ,∴cos2θ(x1x2+y1y2)=-2
,∴cos2θ(x1x2+y1y2)=-2
∴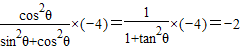 ,
,
解得tanθ=k=±1
∴l:x±y-2=0
点评:本题考查点到直线距离的证明,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.
(Ⅱ)当直线l⊥x轴时,与已知矛盾,设直线方程代入抛物线方程,利用韦达定理,借助于
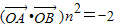 ,可得直线的斜率,从而可得直线l的方程.
,可得直线的斜率,从而可得直线l的方程.解答:(Ⅰ)证明:当A=0,B≠0时,直线l:y=-
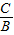 ,点P到直线l的距离d=|
,点P到直线l的距离d=|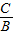 +y|;
+y|;当A≠0,B=0时,直线l:x=-
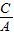 ,点P到直线l的距离d=|
,点P到直线l的距离d=|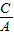 +x|
+x|当AB≠0时,如图,
 则R(
则R(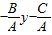 ,y),S(
,y),S(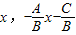 )
)∴PR=|
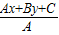 |,PS=|
|,PS=|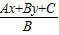 |
|PQ是直角△PRS斜边上的高,由三角形面积公式可得PQ=
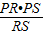 =
=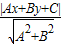
综上知,点P到直线l的距离
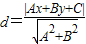 .
.(Ⅱ)解:当直线l⊥x轴时,与已知矛盾;
故可设直线方程:y=k(x-2),A(x1,y1),B(x2,y2)
∴
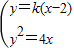 ,∴ky2-4y-8k=0
,∴ky2-4y-8k=0∴
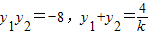 .
.代入抛物线方程可得:
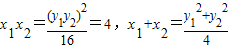
∵
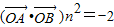 ,∴cos2θ(x1x2+y1y2)=-2
,∴cos2θ(x1x2+y1y2)=-2∴
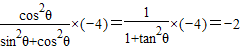 ,
,解得tanθ=k=±1
∴l:x±y-2=0
点评:本题考查点到直线距离的证明,考查直线与抛物线的位置关系,考查向量知识的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目