题目内容
设m,n,t为正数,且P=
,Q=
,S=m+n+t,则( )
| m2+mn+n2 |
| n2+nt+t2 |
| A、Q+S>P |
| B、P+Q>S |
| C、P+S>Q |
| D、P+Q=S |
分析:将P,Q配方,根据
n2> 0
t2>0得到P>m+
n,Q>n+
t,两不等式相加即可.
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵P=
=
>m+
n
Q=
=
>n+
t
∴P+Q>S
故选B
| m2+mn+n2 |
(m+
|
| 1 |
| 2 |
Q=
| n2+nt+t2 |
(n+
|
| 1 |
| 2 |
∴P+Q>S
故选B
点评:本题考查比较两个数的大小,通过配方,利用一个数的平方为正,化简各数.

练习册系列答案
相关题目
 (2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.
(2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.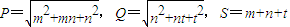 ,则( )
,则( )