题目内容
已知f(x)在(-1,1)上有定义,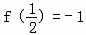 且满足x,y∈(-1,1)时,有
且满足x,y∈(-1,1)时,有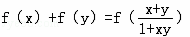
(1)证明:f(x)在(-1,1)上为奇函数.
(2)数列{an}满足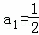 ,
,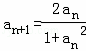 ,xn=f(an),求{xn}的通项公式.
,xn=f(an),求{xn}的通项公式.
(3)求证: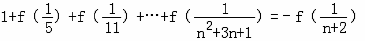 .
.
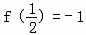 且满足x,y∈(-1,1)时,有
且满足x,y∈(-1,1)时,有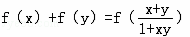
(1)证明:f(x)在(-1,1)上为奇函数.
(2)数列{an}满足
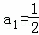 ,
,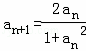 ,xn=f(an),求{xn}的通项公式.
,xn=f(an),求{xn}的通项公式.(3)求证:
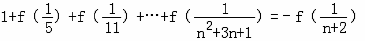 .
.解:(1)证明:令y=0得:f(x)+f(0)=f(x)
所以f(0)=0令y=﹣x
得:f(x)+f(﹣x)=f(0)=0所以f(﹣x)=﹣f(x)
又f(x)的定义域为(﹣1,1) 所以f(x)在(﹣1,1)上为奇函数
(2)解:
∵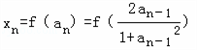
=f(an﹣1)+f(an﹣1)=2f(an﹣1)=2xn﹣1
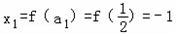
所以{xn}为以2为公比﹣1为首项的等比数列
故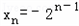
(3)证明:∵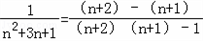 =
=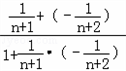 所以:
所以: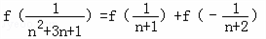 =
=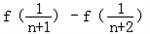
所以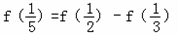
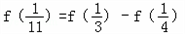 …
…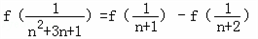
以上等式相加得: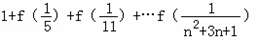 =1+
=1+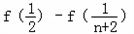 =
=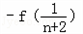
所以f(0)=0令y=﹣x
得:f(x)+f(﹣x)=f(0)=0所以f(﹣x)=﹣f(x)
又f(x)的定义域为(﹣1,1) 所以f(x)在(﹣1,1)上为奇函数
(2)解:
∵
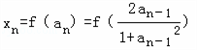
=f(an﹣1)+f(an﹣1)=2f(an﹣1)=2xn﹣1
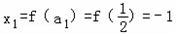
所以{xn}为以2为公比﹣1为首项的等比数列
故
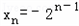
(3)证明:∵
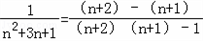 =
=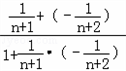 所以:
所以: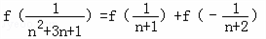 =
=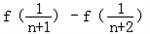
所以
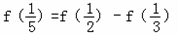
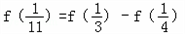 …
…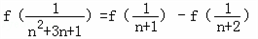
以上等式相加得:
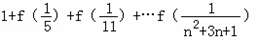 =1+
=1+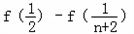 =
=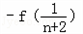

练习册系列答案
相关题目
 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有 .对数列{xn}有
.对数列{xn}有
 <
< 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.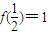 ,且满足x,y∈(-1,1)有
,且满足x,y∈(-1,1)有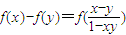 .对数列{xn}有
.对数列{xn}有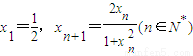
 <
<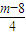 成立?若存在,求出m的最小值.
成立?若存在,求出m的最小值.