题目内容
设函数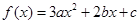 ,且有
,且有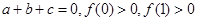 .
.
(1)求证: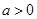 ,且
,且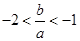 ;
;
(2)求证:函数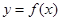 在区间
在区间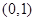 内有两个不同的零点.
内有两个不同的零点.
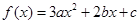 ,且有
,且有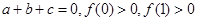 .
.(1)求证:
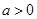 ,且
,且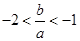 ;
;(2)求证:函数
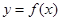 在区间
在区间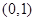 内有两个不同的零点.
内有两个不同的零点.(1)见解析 (2)见解析
试题分析:(1)由
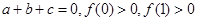 这三个条件联立即可.
这三个条件联立即可.(2)由抛物线
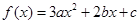 得
得 ;
;  ,
,结合二次函数的图像即可判断.
证明:(1)因为
 ,所以
,所以 , 2分
, 2分由条件
 ,消去
,消去 ,得
,得 ;
;由条件
 ,消去
,消去 ,得
,得 ,即
,即 , 5分
, 5分所以
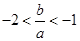 ; 6分
; 6分(2)抛物线
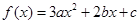 的顶点为
的顶点为 ,
,由
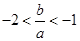 ,得
,得 ,即有
,即有 , 8分
, 8分又因为
 ,
, ,且图象连续不断,
,且图象连续不断,所以函数
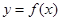 在区间
在区间 与
与 内分别有一个零点,
内分别有一个零点,故函数
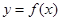 在
在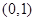 内有两个不同的零点. 12分
内有两个不同的零点. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 .
. ,
, 时,若不等式
时,若不等式 恒成立,求
恒成立,求 的范围;
的范围; 在
在 内存在零点.
内存在零点. ,若
,若 对于所有的
对于所有的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 的三内角分别为
的三内角分别为 ,向量
,向量

 ,记函数
,记函数 .
. ,求
,求 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.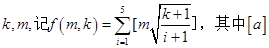 表示不大于a的最大整数,则
表示不大于a的最大整数,则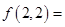 _________.
_________. ,则
,则 ______.
______.