题目内容
设 是两个非零向量,且
是两个非零向量,且 共线,则实数k值为( )
共线,则实数k值为( )A.

B.-

C.

D.8
【答案】分析: 是两个非零向量,且
是两个非零向量,且 ,得出
,得出 不共线,用向量共线的充要条件是存在实数λ,使
不共线,用向量共线的充要条件是存在实数λ,使 及向量相等坐标分别相等列方程解得.
及向量相等坐标分别相等列方程解得.
解答:解:∵ 是两个非零向量,且
是两个非零向量,且 ,得出
,得出 不共线,
不共线,
∵ ,
,
∴存在λ,使得
∴
∴k= .
.
故选C.
点评:本小题主要考查向量的共线定理、向量的垂直、平面向量数量积的运算等基础知识,考查运算求解能力,属于基础题.
 是两个非零向量,且
是两个非零向量,且 ,得出
,得出 不共线,用向量共线的充要条件是存在实数λ,使
不共线,用向量共线的充要条件是存在实数λ,使 及向量相等坐标分别相等列方程解得.
及向量相等坐标分别相等列方程解得.解答:解:∵
 是两个非零向量,且
是两个非零向量,且 ,得出
,得出 不共线,
不共线,∵
 ,
,∴存在λ,使得

∴

∴k=
 .
.故选C.
点评:本小题主要考查向量的共线定理、向量的垂直、平面向量数量积的运算等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
 是两个非零向量,且
是两个非零向量,且
 ,则向量
,则向量 为 .
为 . 是两个非零向量,且
是两个非零向量,且 =
=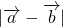 ,则向量
,则向量 与
与 的夹角为
的夹角为 是两个非零向量,且
是两个非零向量,且 =
= ,则向量
,则向量 与
与 的夹角为( )
的夹角为( ) 是两个非零向量,且
是两个非零向量,且 =
= ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )