题目内容

 

    设函数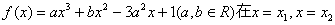处取得极值，且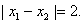

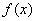   （1）若的值，并求的单调区间；

   （2）若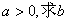的取值范围。

 

 

 

 

【答案】

 解：①……………………1分

（1）当，；

由题意知为方程的两根，

所以的两根，

所以

由……………………3分

从而

当时，

当时，

故在（—1，1）单调递减，在单调递增…………5分

（2）由①式及题意知为方程的两根，

所以，

从而

由止式及题设知…………………………7分

令………………9分

故在单调递增，在单调递减，

从而在的极大值为.

又在上只有一个极值，所以为在上的最大值，

且最小值为

即以值范围为……………………12分

 

练习册系列答案
相关题目
设函数f（x）=ax3+bx2-3a2x+1（a，b∈R）在x=x1，x=x2处取得极值，且|x1-x2|=2．
（Ⅰ）若a=1，求b的值，并求f（x）的单调区间；
（Ⅱ）若a＞0，求b的取值范围．
设f（x）=ax3+bx2+cx（a＞b＞c），已知函数f（x）在x=1处取得极值，且曲线f（x）在x=t处的切线斜率为-2a．
（1）求
c
a
的取值范围；
（2）若函数f（x）的单调递减区间为[m，n]，求|m-n|的最小值；
（3）判断曲线f（x）在x=t-
8
3
处的切线斜率的正负，并说明理由．
设函数f（x）=ax2+bx+
3
4
在x=0处取得极值，且曲线y=f（x）在点（1，f（1））处的切线垂直于直线2x+4y-9=0．
（Ⅰ）求a，b的值；
（Ⅱ）求曲线y=f（x）和直线2x+4y-9=0所围成的封闭图形的面积；
（Ⅲ）设函数g（x）=
ex
f(x)
，若方程g（x）=m有三个不相等的实根，求m的取值范围．
设定义在R上的函数f（x）=ax3+bx2+cx+d满足：①函数f（x）的图象过点P（3，-6）；②函数f（x）在x1、x2处取得极值，且|x1-x2|=4；③函数y=f（x-1）的图象关于点（1，0）对称．
（1）求f（x）的表达式；
（2）若α，β∈R，求证：|f(2cosα)-f(2sinβ)|≤
643
；
（3）求过点P（3，-6）与函数f（x）的图象相切的直线方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网