题目内容
已知四棱锥P-ABCD中,PA⊥平面ABCD,且PA=4PQ=4,底面为直角梯形,∠CDA=∠BAD=90°,AB=2,CD=1,AD=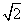 ,M,N分别是PD,PB的中点,
,M,N分别是PD,PB的中点,
(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离。
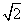 ,M,N分别是PD,PB的中点,
,M,N分别是PD,PB的中点,(1)求证:MQ∥平面PCB;
(2)求截面MCN与底面ABCD所成二面角的大小;
(3)求点A到平面MCN的距离。
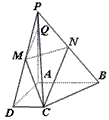
| 解:以A为原点,以AD,AB,AP分别为x,y,z建立空间直角坐标系O-xyz, 由  ,PA=4PQ=4,M,N分别是PD,PB的中点, ,PA=4PQ=4,M,N分别是PD,PB的中点,可得:  , , , ,∴  , , , ,设平面的PBC的法向量为  , ,则有:  , ,令z=1,则  , ,∴  , ,又  平面PCB, 平面PCB,∴MQ∥平面PCB。 (2)设平面的MCN的法向量为  , ,又  , ,则有:  , ,令z=1,则  , ,又  为平面ABCD的法向量, 为平面ABCD的法向量, ∴  , ,又截面MCN与底面ABCD所成二面角为锐二面角, ∴截面MCN与底面ABCD所成二面角的大小为  。 。(3)∵  , ,∴所求的距离  。 。 |
 |

练习册系列答案
相关题目
 如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点.
如图,已知四棱锥P--ABC的底面ABCD为正方形,PA⊥平面ABCD,PA=AB=2,e为PC的中点,F为AD的中点. 如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点.
如图,已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,AB=BC=2CD=2,PB=PC,侧面PBC⊥底面ABCD,O是BC的中点. 已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE.
已知四棱锥P-ABCD的底面是直角梯形,∠ABC=∠BCD=90°,E为BC中点,AE与BD交于O点,AB=BC=2CD=2,BD⊥PE. 如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.
如图,已知四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是直角梯形,∠DAB=∠ABC=90°,E是线段PC上一点,PC⊥平面BDE.