题目内容
 正四棱柱ABCD-A1B1C1D1中,底面边长为2
正四棱柱ABCD-A1B1C1D1中,底面边长为2| 2 |
(1)求证:平面AB1C⊥平面BDD1B1;
(2)求D1到面AB1C的距离;
(3)求三棱锥D1-ACB1的体积V.
分析:(1)由BD⊥AC,BB1⊥AC,BD∩BB1=B?AC⊥平面BDD1B1?平面AB1C⊥平面BDD1B1;
(2)设AC、BD交与点O,连接B1O.点D1作D1H⊥B1O,则D1H即为所求D1到面AB1C的距离;
(3)利用(2)找到的高,再求出底面面积,代入体积计算公式即可.
(2)设AC、BD交与点O,连接B1O.点D1作D1H⊥B1O,则D1H即为所求D1到面AB1C的距离;
(3)利用(2)找到的高,再求出底面面积,代入体积计算公式即可.
解答: (1)证明:∵BD⊥AC,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,
(1)证明:∵BD⊥AC,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,
又因为AC?平面B1EF,所以平面AB1C⊥平面BDD1B1;
(2)解:连接AC、BD交与点O,连接B1O.
过点D1作D1H⊥B1O,则D1H即为所求.
在△B1D1O中,由正四棱柱ABCD-A1B1C1D1中,
底面边长为2
,侧棱长为4.
可得D1O=B1O=
=
=2
,B1D1=4
∴cos∠D1B1O=
=
,
∴
=
=
?B1H=
?D1H=
.
即D1到面AB1C的距离为
.
(3)解:V=
S△AB1C•D1H=
•
•4•2
•
=
.
所以三棱锥D1-ACB1的体积为
.
 (1)证明:∵BD⊥AC,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,
(1)证明:∵BD⊥AC,BB1⊥AC,BD∩BB1=B,∴AC⊥平面BDD1B1,又因为AC?平面B1EF,所以平面AB1C⊥平面BDD1B1;
(2)解:连接AC、BD交与点O,连接B1O.
过点D1作D1H⊥B1O,则D1H即为所求.
在△B1D1O中,由正四棱柱ABCD-A1B1C1D1中,
底面边长为2
| 2 |
可得D1O=B1O=
| DD2+DO2 |
| 20 |
| 5 |
∴cos∠D1B1O=
42+(
| ||||
2×4×
|
| ||
| 10 |
∴
| B1H |
| B1D1 |
| ||
| 10 |
2
| ||
| 5 |
2
| ||
| 5 |
| 8 |
| 5 |
| 5 |
即D1到面AB1C的距离为
8
| ||
| 5 |
(3)解:V=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 8 |
| 5 |
| 5 |
| 32 |
| 3 |
所以三棱锥D1-ACB1的体积为
| 32 |
| 3 |
点评:本题考查平面和平面垂直的判定和性质以及点到面的距离和三棱锥的体积计算公式.是对立体几何知识的综合考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
顶点在同一球面上的正四棱柱ABCD-A′B′C′D′中,AB=1,AA′=
,则A、C两点间的球面距离为( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
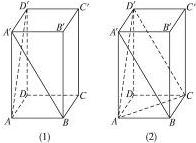 如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是
如图(1),正四棱柱ABCD-A′B′C′D′中,AA′=2AB,则异面直线A′B与AD′所成的角的余弦值是