题目内容
已知向量 =
= ,
, =(cosx-sinx,2sinx),若函数f(x)=
=(cosx-sinx,2sinx),若函数f(x)= •
• .
.
(1)求函数f(x)的单调递增区间;
(2)在△ABC中,a,b,c分别是内角A,B,C的对边,且a=1,b+c=2,f(A)=1,求角A、B、C的大小.
解:(1)∵ =
= ,
, =(cosx-sinx,2sinx)
=(cosx-sinx,2sinx)
∴f(x)=(cosx+sinx)(cosx-sinx)+ cosx•2sinx=cos2x+
cosx•2sinx=cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ),(4分)
),(4分)
令- ≤2x+
≤2x+ ≤
≤ ,即
,即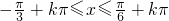 (k∈Z),
(k∈Z),
即函数f(x)的单调递增区间是 (k∈Z);(6分)
(k∈Z);(6分)
(2)因为f(A)=1,所以sin(2x+ )=
)= .
.
∵ <2x+
<2x+ <
< ,
,
∴2x+ =
= ,∴A=
,∴A= .
.
∴cosA= =
=
∵a=1,b+c=2,
∴bc=1
∴b=c=1
∴△ABC为等边三角形,即A=B=C= (12分)
(12分)
分析:(1)利用向量的数量积运算及辅助角公式化简函数,再利用正弦函数的单调递增区间,即可得到结论;
(2)根据f(A)=1,可求A= ,再利用余弦定理及a=1,b+c=2,即可得到结论.
,再利用余弦定理及a=1,b+c=2,即可得到结论.
点评:本题考查向量的数量积运算,考查三角函数的化简,考查函数的性质,同时考查余弦定理的运用,属于中档题.
 =
= ,
, =(cosx-sinx,2sinx)
=(cosx-sinx,2sinx)∴f(x)=(cosx+sinx)(cosx-sinx)+
 cosx•2sinx=cos2x+
cosx•2sinx=cos2x+ sin2x=2sin(2x+
sin2x=2sin(2x+ ),(4分)
),(4分)令-
 ≤2x+
≤2x+ ≤
≤ ,即
,即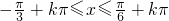 (k∈Z),
(k∈Z),即函数f(x)的单调递增区间是
 (k∈Z);(6分)
(k∈Z);(6分)(2)因为f(A)=1,所以sin(2x+
 )=
)= .
.∵
 <2x+
<2x+ <
< ,
,∴2x+
 =
= ,∴A=
,∴A= .
.∴cosA=
 =
=
∵a=1,b+c=2,
∴bc=1
∴b=c=1
∴△ABC为等边三角形,即A=B=C=
 (12分)
(12分)分析:(1)利用向量的数量积运算及辅助角公式化简函数,再利用正弦函数的单调递增区间,即可得到结论;
(2)根据f(A)=1,可求A=
 ,再利用余弦定理及a=1,b+c=2,即可得到结论.
,再利用余弦定理及a=1,b+c=2,即可得到结论.点评:本题考查向量的数量积运算,考查三角函数的化简,考查函数的性质,同时考查余弦定理的运用,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
 的值.
的值.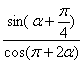 的值.
的值.