题目内容
已知各项均为正数的等比数列{an}满足a2•a4=a6,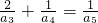 .
.
(Ⅰ)求数列{an}的通项公式an;
(Ⅱ)设数列{an}的前n项和为Sn,前n项积为Tn,求所有的正整数k,使得对任意的n∈N*,不等式Sn+K+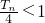 恒成立.
恒成立.
解:(Ⅰ) 设等比数列{an}的首项为a1>0,公比为q>0,
∵a2•a4=a6,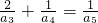 ,
,
∴ ,
,
解得 ,
,
∴ .
.
(Ⅱ)∵ ,
,
∴ =
= =
= ,
,
 =
= ,
,
若存在正整数k,使得不等式 对任意的n∈N*都成立,
对任意的n∈N*都成立,
则 +
+ <1,即
<1,即 ,
,
∵只有当n=1时, 取得最小值2,满足题意.
取得最小值2,满足题意.
∴k<2,正整数k只有取k=1.
分析:(Ⅰ)利用等比数列的通项公式及已知条件即可得出;
(Ⅱ)利用等比数列、等差数列的前n项和公式、指数幂的运算性质、二次函数的单调性即可得出.
点评:本题主要考查等比数列的通项公式及等差、等比数列的求和公式、不等式及其恒成立问题等基础知识,同时考查运算求解能力.
∵a2•a4=a6,
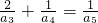 ,
,∴
 ,
,解得
 ,
,∴
 .
.(Ⅱ)∵
 ,
,∴
 =
= =
= ,
, =
= ,
,若存在正整数k,使得不等式
 对任意的n∈N*都成立,
对任意的n∈N*都成立,则
 +
+ <1,即
<1,即 ,
,∵只有当n=1时,
 取得最小值2,满足题意.
取得最小值2,满足题意.∴k<2,正整数k只有取k=1.
分析:(Ⅰ)利用等比数列的通项公式及已知条件即可得出;
(Ⅱ)利用等比数列、等差数列的前n项和公式、指数幂的运算性质、二次函数的单调性即可得出.
点评:本题主要考查等比数列的通项公式及等差、等比数列的求和公式、不等式及其恒成立问题等基础知识,同时考查运算求解能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 中,
中, 与
与 的等比中项为
的等比中项为 ,则
,则 的最小值为( )
的最小值为( ) ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;
是等差数列; 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。