题目内容
海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天从0时至24时的时间x(单位:时)与水深y(单位:米)的关系表:

(1)请选用一个函数来近似描述这个港口的水深与时间的函数关系;
(2)一条货轮的吃水深度(船体最低点与水面的距离)为12米,安全条例规定船体最低点与洋底间隙至少要有1.5米,请问该船何时能进出港口?在港口最多能停留多长时间?
解:(1)以时间为横坐标,水深为纵坐标,考虑用函数y=h+Asin(ωx+φ)刻画水深与时间之间的对应关系.
从数据可以得出:A=3,h=12,T=12,φ=0.
由T= =12,得ω=
=12,得ω= .
.
所以这个港口的水深与时间的关系可用y=12+3sin x,x∈[0,24]近似描述.
x,x∈[0,24]近似描述.
(2)货船需要的安全水深为12+1.5=13.5,所以当y≥13.5时就可以进港.
令12+3sin x≥13.5,∴sin
x≥13.5,∴sin x≥
x≥ .
.
∴2kπ+ ≤
≤ •x≤2kπ+
•x≤2kπ+ ,k∈Z,
,k∈Z,
即12k+1≤x≤12k+5,k∈Z.
∵x∈[0,24],∴1≤x≤5或13≤x≤17.
因此,货船在1点至5点可以进出港;或13点至17点可以进出港.
每次可以在港口最多能停留4小时.
分析:(1)设出函数解析式,据最大值与最小值的差的一半为A;最大值与最小值和的一半为h;通过周期求出ω,得到函数解析式.
(2)据题意列出不等式,利用三角函数的周期性及单调性解三角不等式求出t的范围.
点评:本题考查通过待定系数法求函数解析式、利用三角函数的单调性及周期性解三角不等式.
从数据可以得出:A=3,h=12,T=12,φ=0.
由T=
 =12,得ω=
=12,得ω= .
.所以这个港口的水深与时间的关系可用y=12+3sin
 x,x∈[0,24]近似描述.
x,x∈[0,24]近似描述.(2)货船需要的安全水深为12+1.5=13.5,所以当y≥13.5时就可以进港.
令12+3sin
 x≥13.5,∴sin
x≥13.5,∴sin x≥
x≥ .
.∴2kπ+
 ≤
≤ •x≤2kπ+
•x≤2kπ+ ,k∈Z,
,k∈Z,即12k+1≤x≤12k+5,k∈Z.
∵x∈[0,24],∴1≤x≤5或13≤x≤17.
因此,货船在1点至5点可以进出港;或13点至17点可以进出港.
每次可以在港口最多能停留4小时.
分析:(1)设出函数解析式,据最大值与最小值的差的一半为A;最大值与最小值和的一半为h;通过周期求出ω,得到函数解析式.
(2)据题意列出不等式,利用三角函数的周期性及单调性解三角不等式求出t的范围.
点评:本题考查通过待定系数法求函数解析式、利用三角函数的单调性及周期性解三角不等式.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
(本小题满分12分) 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天从0时至24时的时间![]() (单位:时)与水深y(单位:米)的关系表:
(单位:时)与水深y(单位:米)的关系表:
|
| 0:00 | 3:00 | 6:00 | 9: 00 | 12:00 | 15:00 | 18:00 | 21:00 | 24:00 |
|
| 12.0 | 15.0 | 12.0 | 9.0 | 12.0 | 15.0 | 12.0 | 9.0 | 12.0 |
(1)请选用一个函数来近似描述这个港口的水深与时间的函数关系;
(2)一条货轮的吃水深度(船体最低点与水面的距离)为12米,安全条例规定船体最低点与
洋底间隙至少要有1.5米,请问该船何时能进出港口?在港口最多能停留多长时间?
(本题满分12分)海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地,早潮叫潮,晚潮叫汐. 在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋. 下面是某港口在某季节每天的时间与水深关系表:
|
时刻 |
2:00 |
5:00 |
8:00 |
11:00 |
14:00 |
17:00 |
20:00 |
23:00 |
|
水深(米) |
7.5 |
5.0 |
2.5 |
5.0 |
7.5 |
5.0 |
2.5 |
5.0 |
经长期观测,这个港口的水深与时间的关系,可近似用函数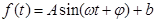
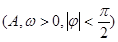 来描述.
来描述.
(1) 根据以上数据,求出函数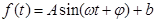 的表达式;
的表达式;
(2) 一条货船的吃水深度(船底与水面的距离)为4.25米,安全条例规定至少要有2米的安全间隙(船底与洋底的距离),该船在一天内(0:00~24:00)何时能进入港口?在港口能停留多久?

