题目内容
某光学仪器厂有一条价值为a万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值.经过市场调查,产品的增加值y万元与技术改造投入x万元之间满足:①y与(a-2x)•x2成正比;
②当
 时,
时, ,并且技术改造投入满足
,并且技术改造投入满足 ,其中t为常数且t∈(1,2].
,其中t为常数且t∈(1,2].(I)求y=f(x)表达式及定义域;
(Ⅱ)求技术改造之后,产品增加值的最大值及相应x的值.
【答案】分析:(I)设y=k(a-2x)x2.由 时,
时, 可得k=4.所以y=4(a-2x)x2,由此能求出函数f(x)的定义域.
可得k=4.所以y=4(a-2x)x2,由此能求出函数f(x)的定义域.
(II)由y=-8x3+4ax2,知 .令y'=0得
.令y'=0得 .因为t∈(1,2],所以
.因为t∈(1,2],所以 .由此能求出技术改造之后,产品增加值的最大值及相应x的值.
.由此能求出技术改造之后,产品增加值的最大值及相应x的值.
解答:解:(I)设y=k(a-2x)x2.
由 时,
时, 可得k=4.
可得k=4.
所以y=4(a-2x)x2.…(3分)
由 ,
,
解得 .
.
所以函数f(x)的定义域为 .…(6分)
.…(6分)
(II)由(I)知y=-8x3+4ax2,
所以 .
.
令y'=0得 .…(8分)
.…(8分)
因为t∈(1,2],
所以 ,即
,即 .
.
当 时,y'>0,函数y=f(x)是增函数;
时,y'>0,函数y=f(x)是增函数;
当 时,y'<0,函数y=f(x)是减函数.…(11分)
时,y'<0,函数y=f(x)是减函数.…(11分)
所以当 时,函数y=f(x)取得最大值,且最大值是
时,函数y=f(x)取得最大值,且最大值是 .…..(13分)
.…..(13分)
所以,1<t≤2时,投入 万元最大增加值
万元最大增加值 万元.…(14分)
万元.…(14分)
点评:本题考查y=f(x)表达式及定义域,求技术改造之后,产品增加值的最大值及相应x的值.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数的性质的灵活运用.
 时,
时, 可得k=4.所以y=4(a-2x)x2,由此能求出函数f(x)的定义域.
可得k=4.所以y=4(a-2x)x2,由此能求出函数f(x)的定义域.(II)由y=-8x3+4ax2,知
 .令y'=0得
.令y'=0得 .因为t∈(1,2],所以
.因为t∈(1,2],所以 .由此能求出技术改造之后,产品增加值的最大值及相应x的值.
.由此能求出技术改造之后,产品增加值的最大值及相应x的值.解答:解:(I)设y=k(a-2x)x2.
由
 时,
时, 可得k=4.
可得k=4.所以y=4(a-2x)x2.…(3分)
由
 ,
,解得
 .
.所以函数f(x)的定义域为
 .…(6分)
.…(6分)(II)由(I)知y=-8x3+4ax2,
所以
 .
.令y'=0得
 .…(8分)
.…(8分)因为t∈(1,2],
所以
 ,即
,即 .
.当
 时,y'>0,函数y=f(x)是增函数;
时,y'>0,函数y=f(x)是增函数;当
 时,y'<0,函数y=f(x)是减函数.…(11分)
时,y'<0,函数y=f(x)是减函数.…(11分)所以当
 时,函数y=f(x)取得最大值,且最大值是
时,函数y=f(x)取得最大值,且最大值是 .…..(13分)
.…..(13分)所以,1<t≤2时,投入
 万元最大增加值
万元最大增加值 万元.…(14分)
万元.…(14分)点评:本题考查y=f(x)表达式及定义域,求技术改造之后,产品增加值的最大值及相应x的值.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化,注意导数的性质的灵活运用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
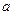 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值 万元与技术改造投入
万元与技术改造投入 万元之间满足:①
万元之间满足:①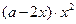 成正比;②当
成正比;②当 时,
时, ,并且技术改造投入满足
,并且技术改造投入满足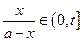 ,其中
,其中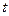 为常数且
为常数且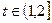 .
. 表达式及定义域;
表达式及定义域;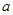 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值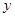 万元与技术改造投入
万元与技术改造投入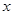 万元之间满足:①
万元之间满足:①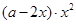 成正比;②当
成正比;②当 时,
时,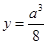 ,并且技术改造投入满足
,并且技术改造投入满足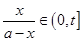 ,其中
,其中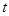 为常数且
为常数且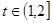 .
.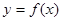 表达式及定义域;
表达式及定义域;