题目内容
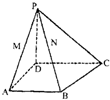 在四棱锥P-ABCD中,AB⊥CD,CD∥AB,PD⊥底面ABCD,AB=
在四棱锥P-ABCD中,AB⊥CD,CD∥AB,PD⊥底面ABCD,AB=| 2 |
(1)求证:直线MN∥平面PDC;
(2)求平面MNCD与平面ABCD所成二面角的大小;
(3)若∠CND=90°,求证:直线DN⊥平面PBC.
分析:(1)根据三角形中位线定理,有线面平行的判定定理,易证直线MN∥平面PDC;
(2)根据PD⊥底面ABCD,结合CD⊥AD可证得CD⊥面PAD,即CD⊥MD.可得∠MAD为平面MNCD与平面ABCD所成二面角的平面角,结合直线PA与底面ABCD成60°,可得答案.
(3)若∠CND=90°,则DN⊥CD,解三角形PAD可得DN⊥PB,由线面垂直的判定定理可得直线DN⊥平面PBC.
(2)根据PD⊥底面ABCD,结合CD⊥AD可证得CD⊥面PAD,即CD⊥MD.可得∠MAD为平面MNCD与平面ABCD所成二面角的平面角,结合直线PA与底面ABCD成60°,可得答案.
(3)若∠CND=90°,则DN⊥CD,解三角形PAD可得DN⊥PB,由线面垂直的判定定理可得直线DN⊥平面PBC.
解答: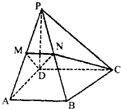 证明:(1)∵M、N是PA、PB中点,
证明:(1)∵M、N是PA、PB中点,
∴MN∥AB,从而MN∥CD.
∵MN在平面PDC外,CD在平面PDC内,
∴直线MN∥平面PDC.
解:(2)∵PD⊥底面ABCD,DC?底面ABCD,
∴PD⊥CD.
又CD∥AB,AB⊥AD,
∴CD⊥AD.
∴CD⊥面PAD.
∴CD⊥MD.
∴∠MAD为平面MNCD与平面ABCD所成二面角的平面角.
∴PD⊥底面ABCD.
∵M是PA的中点,
∴MD=MA.
∴∠MDA=60°.
∴平面MNCD与平面ABCD所成二面角的平面角为60°.
证明:(3)∵AB⊥AD,AB=
AD,
∴BD=
AD.
∵PD⊥底面ABCD,直线PA与底面ABCD成60°角,
∴PD=
AD.
∴PD=BD.
∵N是PB的中点,
∴DN⊥PB.
∵∠CND=90°,
∴DN⊥CD.
∵PB、CN相交于一点N,
∴直线DN⊥平面PBC.
 证明:(1)∵M、N是PA、PB中点,
证明:(1)∵M、N是PA、PB中点,∴MN∥AB,从而MN∥CD.
∵MN在平面PDC外,CD在平面PDC内,
∴直线MN∥平面PDC.
解:(2)∵PD⊥底面ABCD,DC?底面ABCD,
∴PD⊥CD.
又CD∥AB,AB⊥AD,
∴CD⊥AD.
∴CD⊥面PAD.
∴CD⊥MD.
∴∠MAD为平面MNCD与平面ABCD所成二面角的平面角.
∴PD⊥底面ABCD.
∵M是PA的中点,
∴MD=MA.
∴∠MDA=60°.
∴平面MNCD与平面ABCD所成二面角的平面角为60°.
证明:(3)∵AB⊥AD,AB=
| 2 |
∴BD=
| 3 |
∵PD⊥底面ABCD,直线PA与底面ABCD成60°角,
∴PD=
| 3 |
∴PD=BD.
∵N是PB的中点,
∴DN⊥PB.
∵∠CND=90°,
∴DN⊥CD.
∵PB、CN相交于一点N,
∴直线DN⊥平面PBC.
点评:本题考查的知识点是直线与平面平行的判定,直线与平面垂直的判定,二面角的平面角及求法,解答(1)(3)的关键是熟练掌握空间线面关系的判定定理,解得(2)的关键是构造二面角的平面角.

练习册系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点.
如图,在四棱锥P-ABCD中,底面为直角梯形,AD∥BC,∠BAD=90,PA⊥底面ABCD,且PA=AD=AB=2BC=2,M,N分别为PC、PB的中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4.AB=2,AN⊥PC于点N,M是PD中点. 如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点
如图,在四棱锥P-ABCD中,底面ABCD是矩形,O为底面中心,PA⊥平面ABCD,PA=AD=2AB.M是PD的中点 如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形,已知AB=3,AD=2,PA=2,PD=2 (2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,
(2009•成都模拟)如图,在四棱锥P-ABCD中,底面ABCD为正方形,且PD⊥平面ABCD,PD=AB=1,EF分别是PB、AD的中点,