题目内容
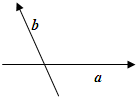已知向量| a |
| b |
（1）试画出
| a |
| b |
| a |
| b |
（2）若|
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
分析：（1）由向量的运算法则作图可得；
（2）由向量的运算可得|
+
|2，进而可得|
+
|，还可得
•(
+
)，而cosθ=
，代入计算即可．
（2）由向量的运算可得|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| ||||||
|
|
解答：
解：（1）如图，以向量
，
为临边作平行四边形ABCD，
可得红色向量
=
+
，绿色向量
=
-
（2）由题意|
|=2，|
|=1，
、
的夹角为120°，
所以|
+
|2=(
+
)2=
2+2
•
+
2
=|
|2+2|
||
|cos120°+|
|2
=22+2×2×1×(-
)+12=3，
∴|
+
|=
又因为
•(
+
)=
2+
•
=|
|2+|
||
|cos120°
=22+2×1×(-
)=3，所以cosθ=
=
=
，
又0°≤θ≤180°，所以θ=30°
解：（1）如图，以向量| a |
| b |
可得红色向量
| AC |
| a |
| b |
| DB |
| a |
| b |
（2）由题意|
| a |
| b |
| a |
| b |
所以|
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| b |
=|
| a |
| a |
| b |
| b |
=22+2×2×1×(-
| 1 |
| 2 |
∴|
| a |
| b |
| 3 |
又因为
| a |
| a |
| b |
| a |
| a |
| b |
| a |
| a |
| b |
=22+2×1×(-
| 1 |
| 2 |
| ||||||
|
|
| 3 | ||
2
|
| ||
| 2 |
又0°≤θ≤180°，所以θ=30°
点评：本题考查数量积与夹角的关系，涉及平面向量的数量积的运算，属中档题．
练习册系列答案
阅读快车系列答案
相关题目
已知向量
