题目内容
已知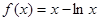 ,
,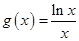 ,其中
,其中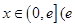 是自然常数).
是自然常数).
(Ⅰ)求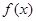 的单调性和极小值;
的单调性和极小值;
(Ⅱ)求证: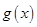 在
在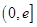 上单调递增;
上单调递增;
(Ⅲ)求证: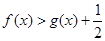 .
.
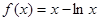 ,
,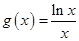 ,其中
,其中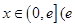 是自然常数).
是自然常数).(Ⅰ)求
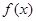 的单调性和极小值;
的单调性和极小值;(Ⅱ)求证:
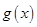 在
在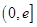 上单调递增;
上单调递增;(Ⅲ)求证:
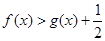 .
.(Ⅰ)当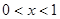 时,
时,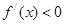 ,此时
,此时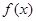 单调递减当
单调递减当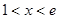 时,
时,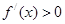 ,此时
,此时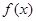 单调递增 ∴
单调递增 ∴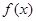 的极小值为
的极小值为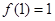
(Ⅱ)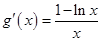 当
当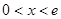 时,
时,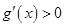 ,
,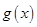 在
在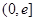 上单调递增
上单调递增
(Ⅲ)略
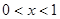 时,
时,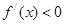 ,此时
,此时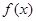 单调递减当
单调递减当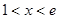 时,
时,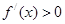 ,此时
,此时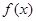 单调递增 ∴
单调递增 ∴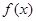 的极小值为
的极小值为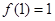
(Ⅱ)
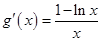 当
当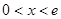 时,
时,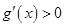 ,
,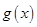 在
在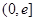 上单调递增
上单调递增 (Ⅲ)略
(1)对函数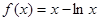 求导,注意定义域,利用导数与函数单调性的关系可求出
求导,注意定义域,利用导数与函数单调性的关系可求出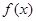 的单调性和极小值;(2)函数
的单调性和极小值;(2)函数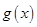 在
在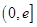 上单调递增;只需证
上单调递增;只需证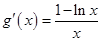 在
在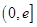 上大于等于0恒成立;(3)由(1)和(2)可得函数
上大于等于0恒成立;(3)由(1)和(2)可得函数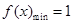 ,
,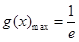 ,因为
,因为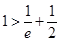 ,所以
,所以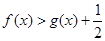
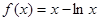 求导,注意定义域,利用导数与函数单调性的关系可求出
求导,注意定义域,利用导数与函数单调性的关系可求出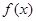 的单调性和极小值;(2)函数
的单调性和极小值;(2)函数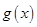 在
在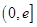 上单调递增;只需证
上单调递增;只需证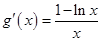 在
在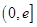 上大于等于0恒成立;(3)由(1)和(2)可得函数
上大于等于0恒成立;(3)由(1)和(2)可得函数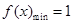 ,
,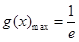 ,因为
,因为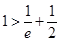 ,所以
,所以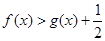

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (
( 且
且 )的图象过点
)的图象过点 ,点
,点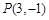 关于直线
关于直线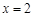 的对称点
的对称点 在
在 的图象上.
的图象上.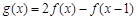 ,求
,求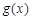 的最小值及取得最小值时x的值.
的最小值及取得最小值时x的值.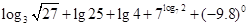 = .
= . 的定义域是
的定义域是 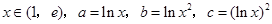 ,则( )
,则( )

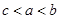

 ,则函数
,则函数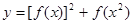 的最大值是____.
的最大值是____. 的的定义域为
的的定义域为 .当
.当 时,求函数
时,求函数 的最值及相应的
的最值及相应的 的值。
的值。 (
( )在
)在 上恒正,则实数a的取值范围为 .
上恒正,则实数a的取值范围为 .