题目内容
已知P(x,y)为函数y=lnx图象上一点,O为坐标原点,记直线OP的斜率为k=f(x).
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求函数F(x)=x-f(x)的最小值.
解:(Ⅰ)k=f(x)= (x>0),求导函数可得f′(x)=
(x>0),求导函数可得f′(x)=
令f′(x)>0,x>0,可得0<x<e;令f′(x)<0,可得x>e
∴f(x)在(0,e)单调递增,(e,+∞)单调递减.
(Ⅱ)F(x)=x- ,求导函数可得F′(x)=
,求导函数可得F′(x)=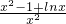
设h(x)=x2-1+lnx,求导函数可得 ------------------(5分)
------------------(5分)
∴h(x)在(0,+∞)为单调递增函数.
∵h(1)=0,∴F'(1)=0,除了1之外,F(x)无其他零点,
∴当x=1时,F(1)=1为最小值.---------------(12分)
分析:(Ⅰ)确定函数k=f(x)= (x>0),求导函数,令f′(x)>0可得函数的单调增区间;令f′(x)<0,可得函数的单调减区间;
(x>0),求导函数,令f′(x)>0可得函数的单调增区间;令f′(x)<0,可得函数的单调减区间;
(Ⅱ)F(x)=x- ,求导函数可得F′(x)=
,求导函数可得F′(x)=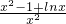 ,构造新函数h(x)=x2-1+lnx,确定h(x)在(0,+∞)为单调递增函数,从而可求函数F(x)=x-f(x)的最小值.
,构造新函数h(x)=x2-1+lnx,确定h(x)在(0,+∞)为单调递增函数,从而可求函数F(x)=x-f(x)的最小值.
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,确定函数解析式是关键.
 (x>0),求导函数可得f′(x)=
(x>0),求导函数可得f′(x)=
令f′(x)>0,x>0,可得0<x<e;令f′(x)<0,可得x>e
∴f(x)在(0,e)单调递增,(e,+∞)单调递减.
(Ⅱ)F(x)=x-
 ,求导函数可得F′(x)=
,求导函数可得F′(x)=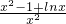
设h(x)=x2-1+lnx,求导函数可得
 ------------------(5分)
------------------(5分)∴h(x)在(0,+∞)为单调递增函数.
∵h(1)=0,∴F'(1)=0,除了1之外,F(x)无其他零点,
∴当x=1时,F(1)=1为最小值.---------------(12分)
分析:(Ⅰ)确定函数k=f(x)=
 (x>0),求导函数,令f′(x)>0可得函数的单调增区间;令f′(x)<0,可得函数的单调减区间;
(x>0),求导函数,令f′(x)>0可得函数的单调增区间;令f′(x)<0,可得函数的单调减区间;(Ⅱ)F(x)=x-
 ,求导函数可得F′(x)=
,求导函数可得F′(x)=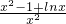 ,构造新函数h(x)=x2-1+lnx,确定h(x)在(0,+∞)为单调递增函数,从而可求函数F(x)=x-f(x)的最小值.
,构造新函数h(x)=x2-1+lnx,确定h(x)在(0,+∞)为单调递增函数,从而可求函数F(x)=x-f(x)的最小值.点评:本题考查导数知识的运用,考查函数的单调性,考查函数的最值,确定函数解析式是关键.

练习册系列答案
相关题目
 已知y=Asin(ωx+?)的最大值为1,在区间[
已知y=Asin(ωx+?)的最大值为1,在区间[| π |
| 6 |
| 2π |
| 3 |
A、(0,
| ||||
B、(0,
| ||||
C、(0,
| ||||
| D、以上都不是 |
 上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )
上,函数值从1减小到-1,函数图象(如图)与y轴的交点P坐标是( )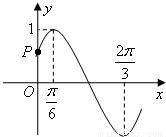



 -2lnx、
-2lnx、