题目内容
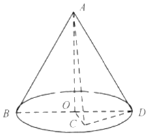
【题目】如图，在三棱锥P—ABC中，平面PAC⊥平面ABC，AB＝BC，PA⊥PC．点E，F，O分别为线段PA，PB，AC的中点，点G是线段CO的中点．
（1）求证：FG∥平面EBO；
（2）求证：PA⊥BE．
【答案】（1）见解析； （2）见解析
【解析】
（1）连接
交
于
，连接
，推导出为
的重心，从而
，由此证得
平面
；
（2）推导出
，从而求得
面
，进而
，再求出
，由此能证得
平面，利用线面垂直的性质，即可得到
.
（1）连接交于，连接，
因为
分别是
的中点，所以为的重心，可得
，
又因为
为线段
的中点，
是线段
的中点，所以
，
所以
，可得，
因为
平面
平面，所以平面.
（2）因为为线段的中点，且
，所以，
因为平面
平面
，平面
平面
平面，
所以平面，又由
平面，所以，
因为
分别为线段
的中点，所以
，
因为
，所以
，
又
平面，所以平面，
因为
平面，所以.
练习册系列答案
高中必刷题系列答案
相关题目
