题目内容
已知焦点在y轴,顶点在原点的抛物线C1经过点P(2,2),以C1上一点C2为圆心的圆过定点A(0,1),记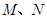 为圆
为圆 与
与 轴的两个交点.
轴的两个交点.
(1)求抛物线 的方程;
的方程;
(2)当圆心 在抛物线上运动时,试判断
在抛物线上运动时,试判断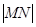 是否为一定值?请证明你的结论;
是否为一定值?请证明你的结论;
(3)当圆心 在抛物线上运动时,记
在抛物线上运动时,记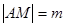 ,
, ,求
,求 的最大值.
的最大值.
(1)x2="2y" ;(2)定值2;(3)
解析试题分析:(1)由焦点在y轴,顶点在原点的抛物线假设为 ,又C1经过点P(2,2),即可求出抛物线的
,又C1经过点P(2,2),即可求出抛物线的 .即可得抛物线的方程.
.即可得抛物线的方程.
(2)当圆心 在抛物线上运动时,写出圆
在抛物线上运动时,写出圆 的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.
的方程,再令y=0即可求得圆的方程与x轴的两交点的坐标,计算两坐标的差即可得到结论.
(3)当圆心 在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心
在抛物线上运动时,由(1)可得M,N的坐标(其中用圆心 的坐标表示).根据两点的距离公式即可用圆心
的坐标表示).根据两点的距离公式即可用圆心 的坐标表示m,n的值,将
的坐标表示m,n的值,将 适当变形,再根据基本不等式即可求得
适当变形,再根据基本不等式即可求得 的最大值.
的最大值.
(1)由已知,设抛物线方程为x2=2py,22=2p×2,解得p=1.
所求抛物线C1的方程为x2=2y.-------3分
(2)法1:设圆心C2(a,a2/2),则圆C2的半径r=
圆C2的方程为 .
.
令y=0,得x2-2ax+a2-1=0,得x1=a-1,x2=a+1.
|MN|=|x1-x2|=2(定值).------7分
法2:设圆心C2(a,b),因为圆过A(0,1),所以半径r= ,
,
,因为C2在抛物线上,a2=2b,且圆被x轴截得的弦长
|MN|= (定值)---7分
(定值)---7分
(3)由(2)知,不妨设M(a-1,0),N(a+1,0),

考点:1.抛物线的性质.2.最值问题.3.基本不等式的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目

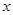 (单位:cm)满足关系:
(单位:cm)满足关系: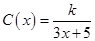 (
(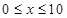 ,
,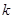 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设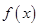 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.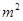 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1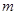 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 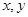 都是正数,
都是正数, ,求
,求 的最大值
的最大值 ,求
,求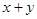 的最小值.
的最小值. ,求函数
,求函数 的最小值;
的最小值; +
+ 的最小值.
的最小值.  为正数,且
为正数,且 的最大值是 。
的最大值是 。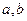 满足
满足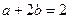 ,则
,则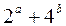 的最小值为__________.
的最小值为__________.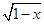 +
+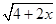 的最大值.
的最大值.