题目内容
在边长2的等边△ABC中,点M为线段BC中点,若P是△ABC所在平面内一点,且
为单位向量,则
•
的最大值为
.
| PA |
| PA |
| PM |
| 3 |
| 3 |
分析:利用点M为线段BC中点,△ABC是边长2的等边,求得|
|,再根据
•
=|
|•|
|cos<
,
>,求最大值.
| AM |
| PA |
| PM |
| PA |
| PM |
| PA |
| PM |
解答:解:∵点M为线段BC中点,△ABC是边长2的等边,
∴|
|=
,
又
为单位向量,
∴
•
=|
|•|
|cos<
,
>=
cos<
,
>≤
,
当向量
与
方向相同时取到最大值.
故答案是:
.
∴|
| AM |
| 3 |
又
| PA |
∴
| PA |
| PM |
| PA |
| PM |
| PA |
| PM |
| 3 |
| PA |
| PM |
| 3 |
当向量
| PA |
| PM |
故答案是:
| 3 |
点评:本题考查向量的数量积公式.解答的关键是利用向量夹角的余弦值的范围求最大值.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
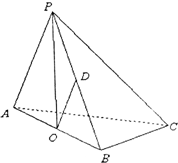 在三棱锥P-ABC中,△PAC和△PBC都是边长为
在三棱锥P-ABC中,△PAC和△PBC都是边长为 的等边三角形,AB=2,O,D分别是AB,PB的中点.
的等边三角形,AB=2,O,D分别是AB,PB的中点.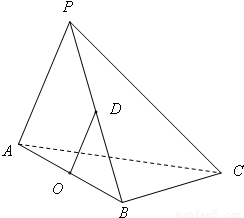 在三棱锥P-ABC中,△PAC和△PBC是边长为
在三棱锥P-ABC中,△PAC和△PBC是边长为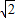 的等边三角形,AB=2,O,D分别是AB,PB的中点.
的等边三角形,AB=2,O,D分别是AB,PB的中点.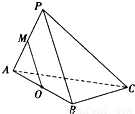 在三棱锥P-ABC中,△PAC和△PBC是边长为
在三棱锥P-ABC中,△PAC和△PBC是边长为 的等边三角形,AB=2,O是AB中点.
的等边三角形,AB=2,O是AB中点.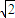 的等边三角形,AB=2,O,D分别是AB,PB的中点.
的等边三角形,AB=2,O,D分别是AB,PB的中点.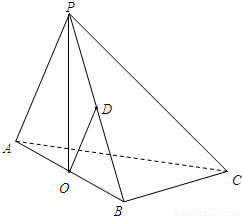
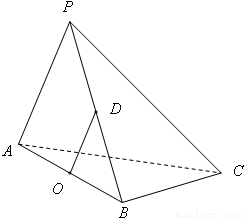 在三棱锥P-ABC中,△PAC和△PBC是边长为
在三棱锥P-ABC中,△PAC和△PBC是边长为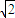 的等边三角形,AB=2,O,D分别是AB,PB的中点.
的等边三角形,AB=2,O,D分别是AB,PB的中点.