题目内容
已知角A、B、C为△ABC的三个内角,其对边分别为a、b、c,若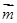 =(-cos
=(-cos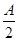 ,sin
,sin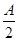 ),
),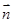 =(cos
=(cos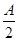 ,sin
,sin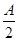 ),a=2
),a=2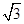 ,且
,且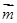 ·
·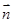 =
=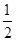 .
.
(1)若△ABC的面积S=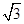 ,求b+c的值.
,求b+c的值.
(2)求b+c的取值范围.
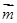 =(-cos
=(-cos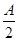 ,sin
,sin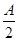 ),
),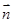 =(cos
=(cos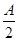 ,sin
,sin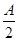 ),a=2
),a=2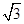 ,且
,且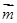 ·
·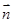 =
=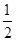 .
.(1)若△ABC的面积S=
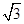 ,求b+c的值.
,求b+c的值.(2)求b+c的取值范围.
(1)4;(2)(2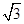 ,4]
,4]
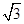 ,4]
,4]试题分析:(1)由
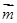 =(-cos
=(-cos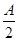 ,sin
,sin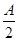 ),
),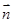 =(cos
=(cos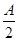 ,sin
,sin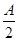 ),且
),且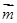 ·
·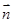 =
=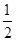 .可求得角A的值,又因为△ABC的面积S=
.可求得角A的值,又因为△ABC的面积S=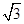 ,a=2
,a=2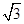 ,在三角形中利用余弦与三角形的面积公式,即可解出b,c的值或者直接构造b+c,即可得到结论.
,在三角形中利用余弦与三角形的面积公式,即可解出b,c的值或者直接构造b+c,即可得到结论.(2)由(1)可知角A,以及边长
 .用角B结合正弦定理分别表示出b,c.再结合角B的范围,求出b+c的取值范围即可.
.用角B结合正弦定理分别表示出b,c.再结合角B的范围,求出b+c的取值范围即可.(1)∵
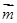 =(-cos
=(-cos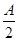 ,sin
,sin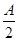 ),
),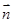 =(cos
=(cos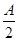 ,sin
,sin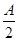 ),且
),且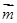 ·
·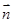 =
=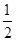 ,
,∴-cos2
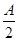 +sin2
+sin2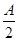 =
=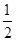 ,即-cosA=
,即-cosA=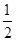 ,
,又A∈(0,π),∴A=
 . …………3分
. …………3分又由S△ABC=
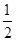 bcsinA=
bcsinA=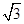 ,所以bc=4,
,所以bc=4,由余弦定理得:a2=b2+c2-2bc·cos
 =b2+c2+bc,
=b2+c2+bc,∴16=(b+c)2,故b+c=4.………7分
(2)由正弦定理得:
 =
= =4,又B+C=p-A=
=4,又B+C=p-A= ,
,∴b+c=4sinB+4sinC=4sinB+4sin(
 -B)=4sin(B+
-B)=4sin(B+ ), 12分
), 12分∵0<B<
 ,则
,则 <B+
<B+ <
< ,则
,则 <sin(B+
<sin(B+ )≤1,即b+c的取值范围是(2
)≤1,即b+c的取值范围是(2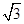 ,4]…..14分
,4]…..14分
练习册系列答案
相关题目
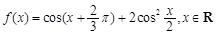 .
.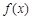 的值域;
的值域;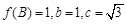 ,求a的值.
,求a的值. 是三内角对应的三边,已知
是三内角对应的三边,已知 .(1)求角A的大小;(2)若
.(1)求角A的大小;(2)若 =
= ,且△ABC的面积为
,且△ABC的面积为 ,求
,求 的值.
的值. 、
、 、
、 、
、 ,欲测量
,欲测量 米,如图,同时也能测量出
米,如图,同时也能测量出 ,
, ,
, ,
, ,则
,则
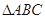 中,
中,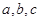 分别是三内角
分别是三内角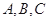 的对边,且
的对边,且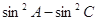 =
=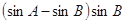 ,则角
,则角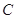 等于( )
等于( )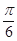
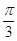
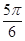
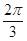
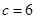 ,
,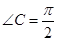 ,且
,且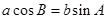 .
.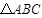 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为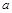 、
、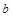 、
、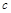 ,已知向量
,已知向量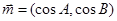 、
、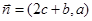 ,且
,且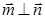 .
.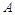 的大小;
的大小;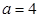 ,求
,求 面积的最大值.
面积的最大值. 中,
中, ,则
,则 ( )
( )


