题目内容
已知函数 是奇函数。
是奇函数。
(1)求实数a的值;
(2)判断函数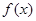 在R上的单调性并用定义法证明;
在R上的单调性并用定义法证明;
(3)若函数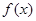 的图像经过点
的图像经过点 ,这对任意
,这对任意 不等式
不等式 ≤
≤ 恒成立,求实数m的范围。
恒成立,求实数m的范围。
(1)-1
(2)利用定义法设作差,然后变形定号来得到证明即可。
(3)
解析试题分析:(1)由 ,得f(0)=0,解得
,得f(0)=0,解得
(2)根据题意,由于函数 是奇函数,那么设
是奇函数,那么设
则可知 ,可知函数
,可知函数
函数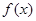 在
在 上为减函数。证明略
上为减函数。证明略
(3) 即
即 即
即
所以由题意 在
在 上恒成立。
上恒成立。
所以
考点:函数单调性
点评:主要是考查了函数单调性以及函数的最值的运用,属于基础题。

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,若
,若 在
在 上为增函数,则称
上为增函数,则称 为“一阶比增函数”.
为“一阶比增函数”.
(Ⅰ) 若 是“一阶比增函数”,求实数
是“一阶比增函数”,求实数 的取值范围;
的取值范围;
(Ⅱ) 若 是“一阶比增函数”,求证:
是“一阶比增函数”,求证: ,
, ;
;
(Ⅲ)若 是“一阶比增函数”,且
是“一阶比增函数”,且 有零点,求证:
有零点,求证: 有解.
有解.
探究函数f(x)=x+ ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;(1)函数f(x)=x+
 (x>0)在区间 上递增.
(x>0)在区间 上递增.当x= 时,y最小= .
(2)证明:函数f(x)=x+
 在区间(0,2)上递减.
在区间(0,2)上递减.(3)思考:函数f(x)=x+
 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)  (
( )在区间
)在区间 上有最大值
上有最大值 和最小值
和最小值 .设
.设 .
. 、
、 的值;
的值; 在
在 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. ,
, )时,f(x)≤g(x),求a的取值范围.
)时,f(x)≤g(x),求a的取值范围.  ,
,
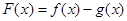 的单调区间;
的单调区间; 时,函数
时,函数 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 满足
满足 .求证:
.求证: .
. ,其中
,其中 ,区间
,区间 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为 ;
; ,当
,当 时,求
时,求 .
. 的单调区间;
的单调区间; 时
时 恒成立,求
恒成立,求 的取值范围。
的取值范围。 有极值,
有极值, 的取值范围;
的取值范围;