题目内容
（x-1）（x-2）…（x-10）的展开式中，x9的系数等于
-55
-55
．分析：展开式中x的一次项系数为每个括号中x的系数与其它括号中的常数项相乘得到的结果，故x9的系数为-（ 1+2+3+4+…+10）运算求得结果
解答：解：（x-1）（x-1）（x-1）…（x-10）展开式中x9的系数为每个括号中的常数项与其它9个括号中的一次项相乘可得
故x9的系数为-（1+2+3+4+…+10）=-55
故答案为：-55
故x9的系数为-（1+2+3+4+…+10）=-55
故答案为：-55
点评：本题主要考查二项式定理，二项展开式的通项公式，求展开式中某项的系数，属于基础题．
练习册系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
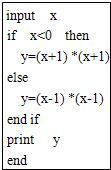为了在运行下面的程序之后得到输出y=9，则键盘输入应该是（ ）input x
if x＜0 then
y=（x+1）*（x+1）
else
y=（x-1）*（x-1）
end if
print y
end
| A、x=-4 | B、x=-2 | C、x=4或x=-4 | D、x=2或x=-2 |
函数y=
+
的定义域是（ ）
| (x+1)0 | ||
|
| 1-6x2+x-2 |
| A、{x|-2≤x＜0} |
| B、{x|-2≤x＜0且x≠-1} |
| C、{x|x≤-2} |
| D、{x|x≥1} |
已知全集U=R，集合M={x|x≥1}，N={x|
≥0}，则?U（M∩N）=（ ）
| x+1 |
| x-2 |
| A、{x|x＜2} |
| B、{x|x≤2} |
| C、{x|-1＜x≤2} |
| D、{x|-1≤x＜2} |