题目内容
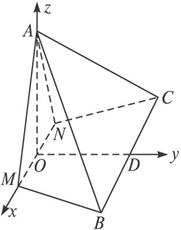
将边长为2的正△ABC沿高AD折成直二面角B-AD-C，则三棱锥B-ACD的外接球的体积是
π
π．
5
| ||
| 6 |
5
| ||
| 6 |
分析：三棱锥B-ACD的三条侧棱BD、DC、DA两两互相垂直，它的外接球就是它扩展为长方体的外接球，求出长方体的对角线的长，就是球的直径，然后求球的体积即可．
解答：解：根据题意可知三棱锥B-ACD的三条侧棱BD、DC、DA两两互相垂直，
所以它的外接球就是它扩展为长方体的外接球，
所以求出长方体的对角线的长为：
=
，
所以球的直径是
，半径为
，
所以球的体积为：
=
π．
故答案为：
π．
所以它的外接球就是它扩展为长方体的外接球，
所以求出长方体的对角线的长为：
1+1 +(
|
| 5 |
所以球的直径是
| 5 |
| ||
| 2 |
所以球的体积为：
| 4πr3 |
| 3 |
5
| ||
| 6 |
故答案为：
5
| ||
| 6 |
点评：本题主要考查了外接球的体积的度量，解题关键将三棱锥B-ACD的外接球扩展为长方体的外接球，属于中档题．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
轴的正半轴上，O为坐标原点.现将正方形OABC绕O点按顺时针方向旋转.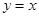
的交点为N.设
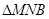的周长为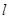
,在正方形OABC旋转的过程中
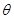，当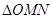
的面积最小？求出这个最小值， 并求出此时△BMN的内切圆半径.
，CD是AB边上的高，E、F分别是AC和BC边的中点．现将△ABC沿CD翻折成直二面角A―DC―B，如图b所示．
