题目内容
已知抛物线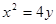 的焦点为
的焦点为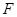 ,过
,过 任作直线
任作直线 (
( 与
与 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于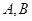 两点,点
两点,点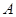 关于
关于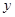 轴对称点为
轴对称点为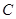 ,
,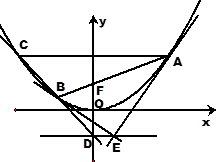
(1)求证:直线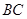 与
与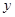 轴交点
轴交点 必为定点;
必为定点;
(2)过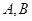 分别作抛物线的切线,两条切线交于
分别作抛物线的切线,两条切线交于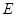 ,求
,求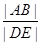 的最小值,并求当
的最小值,并求当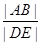 取最小值时直线
取最小值时直线 的方程.
的方程.
(1)通过确定直线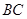 的方程,证明直线
的方程,证明直线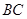 与
与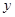 轴交于定点
轴交于定点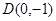 .
.
(2) 或
或 .
.
解析试题分析:(1)通过确定直线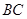 的方程,证明直线
的方程,证明直线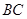 与
与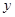 轴交于定点
轴交于定点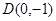 .
.
(2)应用导数的几何意义,确定过点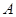 及过点
及过点 的切线方程并联立方程组,确定
的切线方程并联立方程组,确定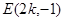 ,
, ,
,
进一步应用“弦长公式”及均值定理,建立 的方程,确定得到
的方程,确定得到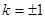 ,从而求得直线
,从而求得直线 的方程为:
的方程为: 或
或 .
.
试题解析:设 ,∵抛物线
,∵抛物线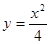 的焦点为
的焦点为
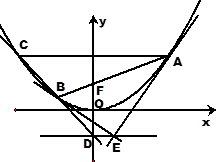
∴可设直线 的方程为:
的方程为:
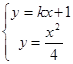 ,消去
,消去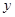 并整理得:
并整理得:
 4分
4分 ,
,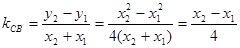
直线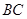 的方程为
的方程为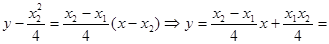

∴直线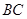 与
与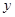 轴交于定点
轴交于定点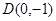 7分
7分
(2) ,∴过点
,∴过点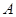 的切线方程为:
的切线方程为: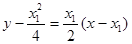
即: ③,同理可得过点
③,同理可得过点 的切线方程为:
的切线方程为: ④ 9分
④ 9分
③—④得: (
( )
)
∴
③+④得:

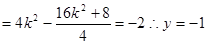 12分
12分
∴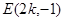 ,
,
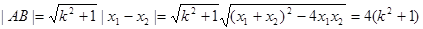
∴ ,取等号时,
,取等号时,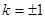 ,
,
直线 的方程为:
的方程为: 或
或 . 15分
. 15分
考点:直线与抛物线的位置关系,导数的几何意义,均值定理的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 轴上,离心率
轴上,离心率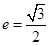 ,点
,点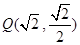 在椭圆C上.
在椭圆C上. 的标准方程;
的标准方程;
 的直线
的直线 交椭圆
交椭圆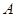 、
、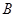 两点,且
两点,且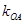 、
、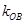 成等差数列,点M(1,1),求
成等差数列,点M(1,1),求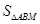 的最大值.
的最大值.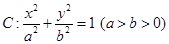 的右焦点为
的右焦点为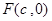 ,上顶点为B,离心率为
,上顶点为B,离心率为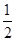 ,圆
,圆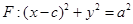 与
与 轴交于
轴交于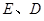 两点
两点 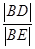 的值;
的值;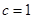 ,过点
,过点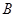 与圆
与圆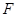 相切的直线
相切的直线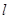 与
与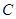 的另一交点为
的另一交点为 ,求
,求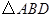 的面积
的面积 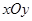 中,点
中,点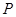 到两点
到两点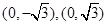 的距离之和等于4,设点
的距离之和等于4,设点 ,直线
,直线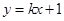 与
与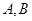 两点.
两点.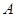 在第一象限,证明当
在第一象限,证明当 时,恒有
时,恒有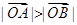 .
.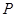 :
: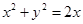 及抛物线
及抛物线 :
: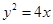 ,过圆心
,过圆心 ,此直线与上述两曲线的四个交点,自上而下顺次记为
,此直线与上述两曲线的四个交点,自上而下顺次记为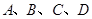 ,如果线段
,如果线段 的长按此顺序构成一个等差数列,求直线
的长按此顺序构成一个等差数列,求直线
 到定点
到定点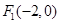 和
和 的距离之和为
的距离之和为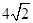 .
. 的方程;
的方程;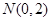 ,过点
,过点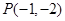 作直线
作直线 ,交椭圆
,交椭圆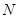 的
的 两点,直线
两点,直线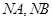 的斜率分别为
的斜率分别为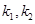 ,证明:
,证明: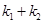 为定值.
为定值.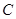 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为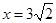 ,离心率为
,离心率为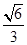 .若直线
.若直线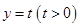 与椭圆
与椭圆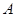 、
、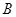 ,以线段
,以线段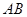 为直径作圆
为直径作圆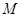 .
.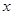 轴相切,求圆
轴相切,求圆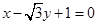 截得的线段长.
截得的线段长.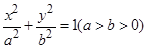 的长轴两端点分别为
的长轴两端点分别为 ,
,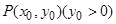 是椭圆上的动点,以
是椭圆上的动点,以 为一边在
为一边在 轴下方作矩形
轴下方作矩形 ,使
,使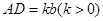 ,
,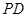 交
交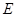 ,
, 交
交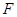 .
.
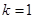 ,且
,且 为椭圆上顶点时,
为椭圆上顶点时,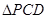 的面积为12,点
的面积为12,点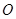 到直线
到直线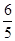 ,求椭圆的方程;
,求椭圆的方程; ,试证明:
,试证明: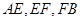 成等比数列.
成等比数列.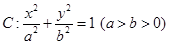 的右焦点为
的右焦点为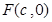 ,上顶点为B,离心率为
,上顶点为B,离心率为 ,圆
,圆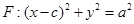 与
与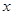 轴交于
轴交于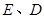 两点
两点 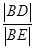 的值;
的值;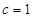 ,过点
,过点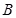 与圆
与圆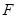 相切的直线
相切的直线 与
与 的另一交点为
的另一交点为 ,求
,求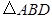 的面积
的面积