题目内容
8.2015年年岁史诗大剧《芈月传》风靡大江南北,影响力不亚于以前的《甄嬛传》.某记者调查了大量《芈月传》的观众,发现年龄段与爱看的比例存在较好的线性相关关系,年龄在[10,14],[15,19],[20,24],[25,29],[30,34]的爱看比例分别为10%,18%,20%,30%,t%.现用这5个年龄段的中间值x代表年龄段,如12代表[10,14],17代表[15,19],根据前四个数据求得x关于爱看比例y的线性回归方程为$\widehaty=(kx-4.68)%$,由此可推测t的值为( )| A. | 33 | B. | 35 | C. | 37 | D. | 39 |
分析 计算前四组数据的平均数,代入线性回归方程求出k的值,再由回归直线方程求出x=32时$\stackrel{∧}{y}$的值即可.
解答 解:前四组数据的平均数为,
$\overline{x}$=$\frac{1}{4}$×(12+17+22+27)=19.5,
$\overline{y}$=$\frac{1}{4}$×(10+18+20+30)=19.5,
代入线性回归方程$\stackrel{∧}{y}$=kx-4.68,
得19.5=k×19.5-4.68,
解得k=1.24,
∴线性回归方程为$\stackrel{∧}{y}$=1.24x-4.68;
当x=32时,$\stackrel{∧}{y}$=1.24×32-4.68≈35,
由此可推测t的值为35.
故选:B.
点评 本题考查了线性回归方程的应用问题,是基础题目.

练习册系列答案
相关题目
16.某地天气预报说:“明天本地降雨的概率为80%”,这是指( )
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
20.等比数列{an}中,a1>1,前n项和为Sn,若$\lim_{x→∞}{S_n}=\frac{1}{a_1}$,那么a1的取值范围是( )
| A. | (1,+∞) | B. | (1,2) | C. | $(1\;,\;\;\sqrt{3})$ | D. | $(1\;,\;\;\sqrt{2})$ |
17.已知函数f(x)=2sin(ωx+φ)+1(ω>0,|φ|≤$\frac{π}{2}}$),其图象与直线y=2最近的两个相邻交点间的距离为$\frac{π}{3}$,若f(x)>1对$?x∈({-\frac{π}{8},\frac{π}{3}})$恒成立,则φ的取值范围是( )
| A. | $[{\frac{π}{4},\frac{π}{3}}]$ | B. | $[{-\frac{π}{6},\frac{π}{4}}]$ | C. | $[{\frac{π}{6},\frac{π}{4}}]$ | D. | $({\frac{π}{6},\frac{π}{2}}]$ |
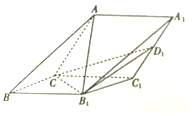 如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.
如图,在三棱锥ABC-A1B1C1中,侧面ACC1A1与侧面CBB1C1都是菱形,∠ACC1=∠CC1B1=60°,AC=2$\sqrt{3}$.