题目内容
设向量 =(sinx,cosx),
=(sinx,cosx), =(cosx,cosx),x∈R,函数f(x)=
=(cosx,cosx),x∈R,函数f(x)=
(1)求函数f(x)的最小正周期;
(2)当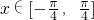 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(3)求使不等式f(x)≥1成立的x的取值范围.
解:(1)∵ =(sinx-cosx,0),
=(sinx-cosx,0),
∴ =(sinx,cosx)•(sinx-cosx,0)
=(sinx,cosx)•(sinx-cosx,0)
=sin2x-sinxcosx= ,所以周期 T=
,所以周期 T= =π.
=π.
(2)当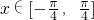 时,-
时,- ,-
,- ,
,
所以 ,即
,即 ≤f(x)≤1.
≤f(x)≤1.
(3)f(x)≥1,即 ,所以
,所以 ,
,
 +2kπ,k∈Z,所以
+2kπ,k∈Z,所以 +kπ,k∈Z,
+kπ,k∈Z,
所以x∈ .
.
分析:(1)利用两个向量的数量积公式,三角恒等变换,化简函数的解析式为 ,求得周期.
,求得周期.
(2)根据x的范围,求得角2x+ 的范围,即可得到sin(2x+
的范围,即可得到sin(2x+ )的 范围,进而求得函数的值域.
)的 范围,进而求得函数的值域.
(3)不等式可化为 ,由
,由 ,可求得x的取值范围.
,可求得x的取值范围.
点评:本题考查两个向量的数量积公式,三角恒等变换,正弦函数的周期性、单调性、定义域、值域的求法,化简函数的解析式
为 ,是解题的突破口.
,是解题的突破口.
 =(sinx-cosx,0),
=(sinx-cosx,0),∴
 =(sinx,cosx)•(sinx-cosx,0)
=(sinx,cosx)•(sinx-cosx,0)=sin2x-sinxcosx=
 ,所以周期 T=
,所以周期 T= =π.
=π.(2)当
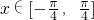 时,-
时,- ,-
,- ,
,所以
 ,即
,即 ≤f(x)≤1.
≤f(x)≤1.(3)f(x)≥1,即
 ,所以
,所以 ,
, +2kπ,k∈Z,所以
+2kπ,k∈Z,所以 +kπ,k∈Z,
+kπ,k∈Z,所以x∈
 .
.分析:(1)利用两个向量的数量积公式,三角恒等变换,化简函数的解析式为
 ,求得周期.
,求得周期.(2)根据x的范围,求得角2x+
 的范围,即可得到sin(2x+
的范围,即可得到sin(2x+ )的 范围,进而求得函数的值域.
)的 范围,进而求得函数的值域.(3)不等式可化为
 ,由
,由 ,可求得x的取值范围.
,可求得x的取值范围.点评:本题考查两个向量的数量积公式,三角恒等变换,正弦函数的周期性、单调性、定义域、值域的求法,化简函数的解析式
为
 ,是解题的突破口.
,是解题的突破口. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设向量
=(sinx,
),
=(
,2cosx)且
∥
,则锐角x为( )
| a |
| 3 |
| 2 |
| b |
| 2 |
| 3 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|