题目内容
在直角坐标系中,动点M到点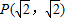 的距离等于点M到直线
的距离等于点M到直线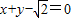 的距离的
的距离的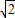 倍,记动点M的轨迹为W,过点A(a,0)(a>0)作一条斜率为k(k<0)的直线交曲线W于B,C两点,且交y轴于点D.
倍,记动点M的轨迹为W,过点A(a,0)(a>0)作一条斜率为k(k<0)的直线交曲线W于B,C两点,且交y轴于点D.(1)求动点M的轨迹,并指出它的三条性质或特征;
(2)求证:|AB|=|CD|;
(3)若|BC|=|BD|,求△OAD的面积.(O为坐标原点)
【答案】分析:(1)直接根据动点M到点 的距离等于点M到直线
的距离等于点M到直线 的距离的
的距离的 倍,整理可得动点M的轨迹方程为为xy=1双曲线,再根据双曲线的性质写出其性质即可;
倍,整理可得动点M的轨迹方程为为xy=1双曲线,再根据双曲线的性质写出其性质即可;
(2)直线方程为y=k(x-a),联立直线方程与双曲线方程整理求出BC中点以及AD的中点,只要中点坐标相同即可说明结论.
(3)先根据|BC|=|BD|,得到x2=2x1,结合上面的结论得到k和a之间的关系,再代入三角形的面积公式整理即可得到结论.
解答:解:(1)设M(x,y),
依题意有: .化简得xy=1.
.化简得xy=1.
即动点M的轨迹方程为xy=1双曲线,其性质为 (4分)
(1)焦点( )(2)实轴长2
)(2)实轴长2 (3)虚轴长2
(3)虚轴长2
(4)对称性y=±x,(0,0)(5)渐近线x=0,y=0等 (8分)
(2)直线方程为y=k(x-a),由 得
得
kx2-kax-1=0.
设B(x1,y1),C(x2,y2),BC中点为N(x,y),
 .
.
又D(0,-ka)
∴ .
.
由|AN|=|DN|,|BN|=|CN|,
可得|AB|=|CD|(14分)
(3)若|BC|=|BD|,可知x1<x2,
则x1=x2-x1,即x2=2x1,
 ,
,
 .
.
又|OA|=a,|OD|=-ka,
∴S△OCD= .(18分)
.(18分)
点评:本题主要考查轨迹方程的求法以及直线与圆锥曲线的位置关系.解决本题的关键在于根据动点M到点 的距离等于点M到直线
的距离等于点M到直线 的距离的
的距离的 倍,整理得到动点M的轨迹方程.
倍,整理得到动点M的轨迹方程.
 的距离等于点M到直线
的距离等于点M到直线 的距离的
的距离的 倍,整理可得动点M的轨迹方程为为xy=1双曲线,再根据双曲线的性质写出其性质即可;
倍,整理可得动点M的轨迹方程为为xy=1双曲线,再根据双曲线的性质写出其性质即可;(2)直线方程为y=k(x-a),联立直线方程与双曲线方程整理求出BC中点以及AD的中点,只要中点坐标相同即可说明结论.
(3)先根据|BC|=|BD|,得到x2=2x1,结合上面的结论得到k和a之间的关系,再代入三角形的面积公式整理即可得到结论.
解答:解:(1)设M(x,y),
依题意有:
 .化简得xy=1.
.化简得xy=1.即动点M的轨迹方程为xy=1双曲线,其性质为 (4分)
(1)焦点(
 )(2)实轴长2
)(2)实轴长2 (3)虚轴长2
(3)虚轴长2
(4)对称性y=±x,(0,0)(5)渐近线x=0,y=0等 (8分)
(2)直线方程为y=k(x-a),由
 得
得kx2-kax-1=0.
设B(x1,y1),C(x2,y2),BC中点为N(x,y),
 .
.又D(0,-ka)
∴
 .
.由|AN|=|DN|,|BN|=|CN|,
可得|AB|=|CD|(14分)
(3)若|BC|=|BD|,可知x1<x2,
则x1=x2-x1,即x2=2x1,
 ,
, .
.又|OA|=a,|OD|=-ka,
∴S△OCD=
 .(18分)
.(18分)点评:本题主要考查轨迹方程的求法以及直线与圆锥曲线的位置关系.解决本题的关键在于根据动点M到点
 的距离等于点M到直线
的距离等于点M到直线 的距离的
的距离的 倍,整理得到动点M的轨迹方程.
倍,整理得到动点M的轨迹方程. 
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
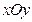 中,动点P到两定点
中,动点P到两定点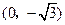 ,
,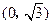 的距离之和等于4,设动点P的轨迹为
的距离之和等于4,设动点P的轨迹为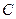 ,过点
,过点 中,动点
中,动点 与定点
与定点 的距离和它到定直线
的距离和它到定直线 的距离之比是
的距离之比是 ,设动点
,设动点 ,
, 是动圆
是动圆
 上一点.
上一点. 与点
与点 的距离成等差数列,若线段
的距离成等差数列,若线段 的垂直平分线与
的垂直平分线与 轴的交点为
轴的交点为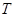 ,求直线
,求直线 的斜率
的斜率 ;
; 与
与 均只有一个公共点,求
均只有一个公共点,求 的最大值.
的最大值. 中,动点
中,动点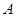 ,
,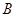 分别在射线
分别在射线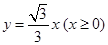 和
和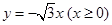 上运动,且△
上运动,且△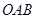 的面积为
的面积为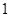 .则点
.则点