题目内容
（本小题共12分）
在直角坐标系
中，动点P到两定点
，
的距离之和等于4，设动点P的轨迹为
，过点的直线与交于A，B两点．
（1）写出的方程；
（2）设d为A、B两点间的距离，d是否存在最大值、最小值；若存在， 求出d的最大值、最小值．
, d的最大值、最小值存在，分别为4、1
解析:
解：（1）设P( x，y )，由椭圆定义可知，点P的轨迹C是以
，
为焦点，长半轴为2的椭圆．它的短半轴
，
故曲线C的方程为． ……4分
（2）① 设过点的直线方程为y=kx+
,
，
其坐标满足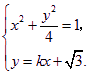
消去y并整理得
. ……6分
∴ 
。
∴ 
=4
=
。
∵
，∴k=0时，d取得最小值1 。……10分
② 当k不存在时,过点的直线方程为x=0,此时交点A、B分别为椭圆C的长轴的两端点，
∴d取最大值4. ……12分
综上, d的最大值、最小值存在，分别为4、1．……12分
练习册系列答案
阅读快车系列答案
相关题目
的焦点坐
标为
（
），点M（
，
）在椭圆E上
（1）求椭圆E的方程；（2）O为坐标原点，⊙
的任意一条切线与椭圆E有两个交点
，
且
，求⊙
⊥平面
，
∥
是正三角形，
，且
是
的中点
∥平面
；
．
名，女同学有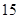
名，老师按照分层抽样的方法组建了一个
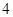人的课外兴趣小组．
名同学做实验，该同学做完后，再从小组内剩下的同学中选一名同学做实验，求选出的两名同学中恰有一名女同学的概率；
，
，求证：
.
的值.