题目内容
下图是指数函数:①y=ax;②y=bx;③y=cx;④y=dx的图象,则a、b、c、d与1的大小关系是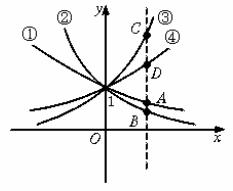
A.a<b<1<c<d B.b<a<1<d<c
C.1<a<b<c<d D.a<b<1<d<c
解法一:在①②中底数小于1且大于零,在y轴右边,底数越小,图象越靠近x轴,故有b<a.在③④中底数大于1,底数越大图象越靠近y轴,故有d<c.∴选B.
解法二:设x=1与①②③④的图象分别交于点A、B、C、D,则其坐标依次为(1,a)、(1,b)、(1,c)、(1,d),由图象观察可得c>d>1>a>b.故选B.
答案:B
点评:当指数函数底数大于1时,图象上升,且当底数越大,图象向上越靠近于y轴,当底数大于0小于1时,图象下降,底数越小,图象向下越靠近于x轴,简称x>0时,底大图象高.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目




