Question

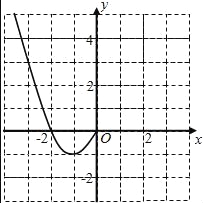
【题目】已知函数，

（1）若，求函数的零点；

（2）若函数在区间上恰有一个零点，求的取值范围．

Answer 1

【答案】（1）1（2）

【解析】

试题分析：（1）利用零点的含义、一元二次方程的解法即可得出；（2）对f（x）进行分解，得到和，进而可得到a的取值范围

试题解析：（1）若，则， 由=0，

得， 解得，

∴当时，函数的零点是1.

（2）已知函数

①当时，，由得，

∴当时，函数在区间上恰有一个零点.

当时，

②若，则，由（1）知函数的零点是，

∴当时，函数在区间上恰有一个零点.

③若，则,

由,

解得，即 ,

∴函数在区间上必有一个零点.

要使函数在区间上恰有一个零点.

必须 ，或 ,

解得 ,

又∵或,

∴或,

综合①②③得，的取值范围是