题目内容
设数列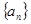 是等差数列,且
是等差数列,且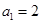 且
且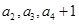 成等比数列。
成等比数列。
(1).求数列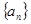 的通项公式
的通项公式
(2).设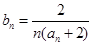 ,求前n项和
,求前n项和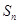 .
.
(1)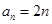 ;(2)
;(2) .
.
解析试题分析:本题主要考查等差数列的通项公式、数列求和、解方程等基础知识,意在考查考生的运算求解能力、基本量思想和利用裂项相消法的解题能力.第一问,利用等比中项将数学语言写成数学表达式,再利用等差数列的通项公式将 展开,通过解方程,解出基本量
展开,通过解方程,解出基本量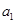 和
和 ,而此题
,而此题 有2个值,需通过已知条件验证舍掉一个,从而得到等差数列的通项公式;第二问,利用第一问的结论,代入到
有2个值,需通过已知条件验证舍掉一个,从而得到等差数列的通项公式;第二问,利用第一问的结论,代入到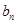 中,用裂项相消法求和.
中,用裂项相消法求和.
试题解析:(1)设等差数列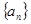 的公差为
的公差为 ,又
,又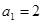
则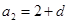 ,
,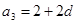 ,
,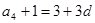 ,
,
又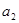 ,
,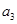 ,
,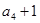 成等比数列.
成等比数列.
∴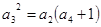 ,即
,即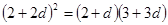 ,
,
解得 或
或 , 4分
, 4分
又 时,
时,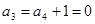 ,与
,与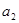 ,
,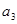 ,
, 成等比数列矛盾,
成等比数列矛盾,
∴ ,∴
,∴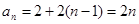 ,即
,即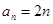 . 6分
. 6分
(2)因为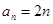 ,∴
,∴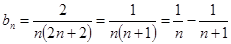 8分
8分
∴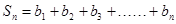
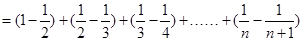
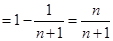 .
.
12分
考点:等差数列的通项公式、数列求和、解方程.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
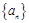 中,
中,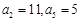 .
.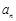 ;
; 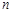 项和
项和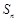 的最大值.
的最大值.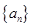 的首项
的首项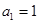 ,公差
,公差 ,且
,且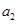 、
、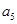 、
、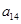 分别是等比数列
分别是等比数列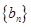 的
的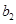 、
、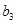 、
、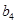 .
.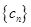 对任意正整数
对任意正整数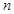 均有
均有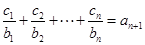 成立,求
成立,求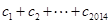 的值.
的值.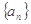 ,等比数列
,等比数列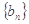 ,满足
,满足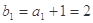 ,
,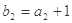 ,
,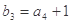 .
.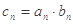 ,求数列{
,求数列{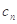 }的前n项和.
}的前n项和.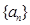 中抽出一些项,依原来的顺序组成的新数列叫数列
中抽出一些项,依原来的顺序组成的新数列叫数列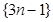 的一个是等比数列的子列;
的一个是等比数列的子列;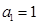 ,公比为
,公比为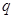 .求证:当
.求证:当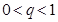 时,数列
时,数列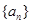 的各项均为正数,
的各项均为正数,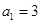 ,前项和为
,前项和为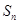 ,
,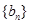 为等比数列,
为等比数列, 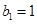 ,且
,且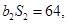
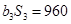 . (1)求
. (1)求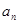 与
与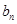 ;
; 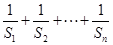 .
.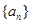 是公差不为0的等差数列,
是公差不为0的等差数列,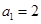 ,且
,且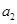 ,
,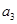 ,
,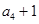 成等比数列.
成等比数列.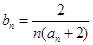 ,求数列
,求数列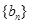 的前
的前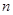 项和
项和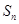 。
。