题目内容
等差数列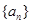 的各项均为正数,
的各项均为正数,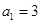 ,前项和为
,前项和为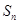 ,
,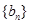 为等比数列,
为等比数列, 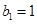 ,且
,且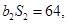
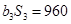 . (1)求
. (1)求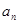 与
与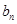 ;
;
(2)求和: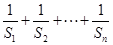 .
.
(1) ;
;
(2)
 .
.
解析试题分析:(1)设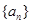 的公差为
的公差为 ,
,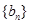 的公比为
的公比为 ,则
,则 为正整数,
为正整数,
依题意可建立 的方程组.注意根据题意舍去增解,得到通项公式.
的方程组.注意根据题意舍去增解,得到通项公式.
(2)注意到 ,
,
因此,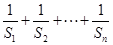 可利用“裂项相消法”求和,问题难度不大,但较为典型,
可利用“裂项相消法”求和,问题难度不大,但较为典型,
应注意熟练掌握解题方法.
试题解析:(1)设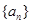 的公差为
的公差为 ,
,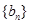 的公比为,则
的公比为,则 为正整数,
为正整数, ,
,
依题意有 ①
①
解得 或
或 (舍去) 4分
(舍去) 4分
故 6分
6分
(2) 8分
8分
∴ 10
10 

 12分
12分
若结果不化简也得分
考点:等差数列,等比数列,“裂项相消法”.

练习册系列答案
相关题目
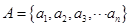 ,
,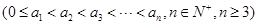
 :对任意的
:对任意的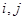
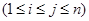 ,
,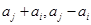 至少有一个属于
至少有一个属于 .
.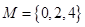 与
与 是否具有性质
是否具有性质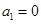 ;
;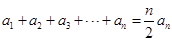 ;
;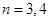 或
或 时集合
时集合 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.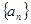 满足
满足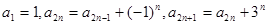 (
( ).
). 的值;
的值;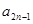 (用含
(用含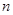 的式子表示);
的式子表示); ,数列
,数列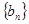
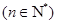 的前
的前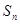 ,求
,求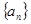 是等差数列,且
是等差数列,且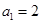 且
且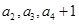 成等比数列。
成等比数列。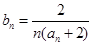 ,求前n项和
,求前n项和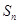 .
.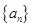 是首项和公比均为
是首项和公比均为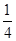 的等比数列,设
的等比数列,设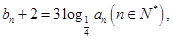 .
.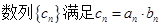
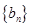 是等差数列;
是等差数列;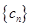 的前n项和
的前n项和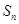 .
.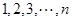 中这
中这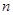 个数中取
个数中取 (
( ,
,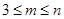 )个数组成递增等差数列,所有可能的递增等差数列的个数记为
)个数组成递增等差数列,所有可能的递增等差数列的个数记为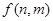 .
.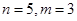 时,写出所有可能的递增等差数列及
时,写出所有可能的递增等差数列及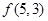 的值;
的值;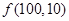 ;
;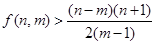 .
.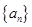 的前
的前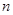 项和
项和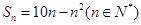 ,又
,又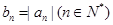 ,求数列
,求数列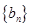 的前
的前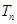 .
.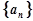 的前n项和为
的前n项和为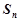 ,
,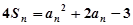 ,且
,且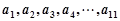 成等比数列,当
成等比数列,当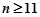 时,
时,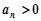 .
.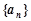 成等差数列;
成等差数列;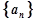 的前n项和
的前n项和