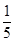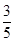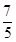题目内容
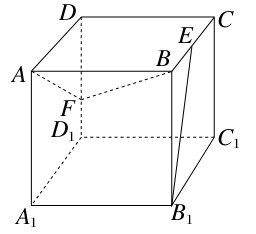
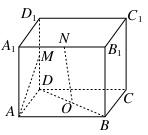
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
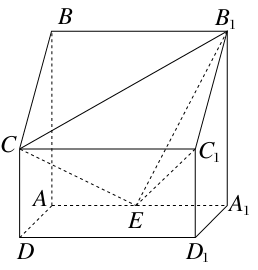
(1)证明:B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为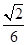 ,求线段AM的长.
,求线段AM的长.

(1)证明:B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为
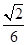 ,求线段AM的长.
,求线段AM的长.(1)见解析 (2)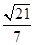 (3)
(3)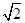
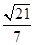 (3)
(3)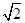
解:本题可通过建立空间坐标系求解.
如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).

(1)证明:易得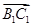 =(1,0,-1),
=(1,0,-1),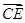 =(-1,1,-1),于是
=(-1,1,-1),于是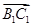 ·
·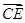 =0,∴B1C1⊥CE.
=0,∴B1C1⊥CE.
(2)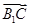 =(1,-2,-1).
=(1,-2,-1).
设平面B1CE的法向量m=(x,y,z),
则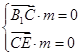 ,即
,即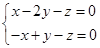
消去x,得y+2z=0,不妨令z=1,可得一个法向量为m=(-3,-2,1).
由(1),B1C1⊥CE,又CC1⊥B1C1,可得B1C1⊥平面CEC1,故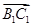 =(1,0,-1)为平面CEC1的一个法向量.
=(1,0,-1)为平面CEC1的一个法向量.
于是cos〈m,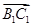 〉=
〉=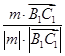 =
=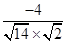 =-
=-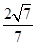 ,从而sin〈m,
,从而sin〈m,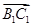 〉=
〉=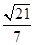 ,
,
故二面角B1-CE-C1的正弦值为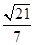 .
.
(3)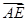 =(0,1,0),
=(0,1,0),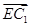 =(1,1,1).
=(1,1,1).
设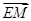 =λ
=λ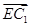 =(λ,λ,λ),0≤λ≤1,有
=(λ,λ,λ),0≤λ≤1,有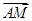 =
=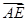 +
+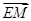 =(λ,λ+1,λ).可取
=(λ,λ+1,λ).可取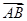 =(0,0,2)为平面ADD1A1的一个法向量.
=(0,0,2)为平面ADD1A1的一个法向量.
设θ为直线AM与平面ADD1A1所成的角,则
sinθ=|cos〈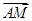 ,
,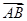 〉|=
〉|=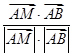
=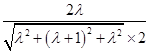 =
=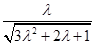 .
.
于是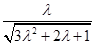 =
=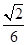 ,解得λ=
,解得λ=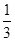 (λ=-
(λ=-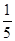 舍去),
舍去),
∴AM=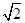 .
.
如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),B(0,0,2),C(1,0,1),B1(0,2,2),C1(1,2,1),E(0,1,0).

(1)证明:易得
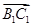 =(1,0,-1),
=(1,0,-1),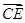 =(-1,1,-1),于是
=(-1,1,-1),于是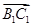 ·
·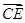 =0,∴B1C1⊥CE.
=0,∴B1C1⊥CE.(2)
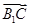 =(1,-2,-1).
=(1,-2,-1).设平面B1CE的法向量m=(x,y,z),
则
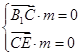 ,即
,即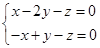
消去x,得y+2z=0,不妨令z=1,可得一个法向量为m=(-3,-2,1).
由(1),B1C1⊥CE,又CC1⊥B1C1,可得B1C1⊥平面CEC1,故
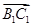 =(1,0,-1)为平面CEC1的一个法向量.
=(1,0,-1)为平面CEC1的一个法向量.于是cos〈m,
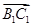 〉=
〉=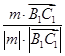 =
=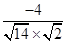 =-
=-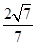 ,从而sin〈m,
,从而sin〈m, 〉=
〉=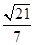 ,
,故二面角B1-CE-C1的正弦值为
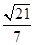 .
.(3)
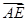 =(0,1,0),
=(0,1,0),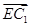 =(1,1,1).
=(1,1,1).设
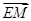 =λ
=λ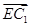 =(λ,λ,λ),0≤λ≤1,有
=(λ,λ,λ),0≤λ≤1,有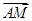 =
=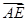 +
+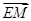 =(λ,λ+1,λ).可取
=(λ,λ+1,λ).可取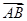 =(0,0,2)为平面ADD1A1的一个法向量.
=(0,0,2)为平面ADD1A1的一个法向量.设θ为直线AM与平面ADD1A1所成的角,则
sinθ=|cos〈
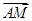 ,
,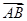 〉|=
〉|=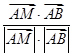
=
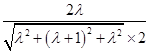 =
=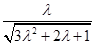 .
.于是
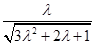 =
=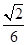 ,解得λ=
,解得λ=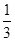 (λ=-
(λ=-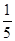 舍去),
舍去),∴AM=
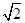 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
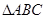 和
和 所在平面互相垂直,且
所在平面互相垂直,且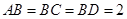 ,
,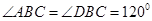 ,E、F分别为AC、DC的中点.
,E、F分别为AC、DC的中点.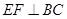 ;
;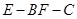 的正弦值.
的正弦值.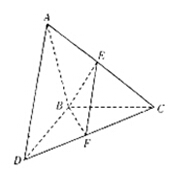
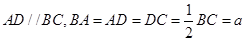 ,E是BC的中点,将△BAE沿AE翻折成
,E是BC的中点,将△BAE沿AE翻折成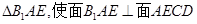 ,F为
,F为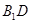 的中点.
的中点.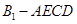 的体积;
的体积;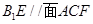 ;
; 所成锐二面角的余弦值.
所成锐二面角的余弦值.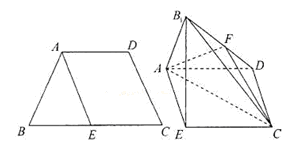
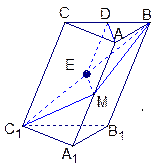
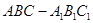 的各棱长均为2,侧棱
的各棱长均为2,侧棱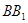 与底面
与底面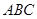 所成的角为
所成的角为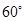 ,
,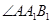 为锐角,且侧面
为锐角,且侧面 ⊥底面
⊥底面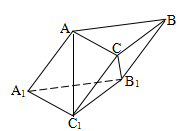
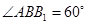 ;
;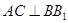 ;
;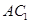 与平面
与平面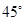 ;
;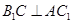 .
.