题目内容
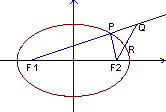
已知椭圆
=1,点P为其上一点，F1、F2为椭圆的焦点，Q为射线
延长线上一点，且|PQ|=|PF2|，设R为F2Q的中点。
(1)当P点在椭圆上运动时，求R形成的轨迹方程；
(2)设点R形成的曲线为C，直线l：y=k(x+4
)与曲线C相交于A、B两点，若∠AOB=90o时，
求k的值.
（请注意把答案填写在答题卡上）
解：(1) F1(－2,0),F2(2,0) 设R(x,y）,Q(x1,y1). ∵|PQ|=|PF2|，
∴|F1Q|=|F2P|+|PQ|=|F1P|+|PF2|=8,则(x1+2)2+y12=64.------4分
又
得x1=2x+2,y1=2y.
∴(2x)2+(2y)2=64， 故R的轨迹方程为：x2+y2=16------------7分
(2)如右图，当∠AOB=90°时，在Rt△AOC中，∠AOC=45°，此时弦心距|OC|=
又|OC|=
. 由=得
-----------12分
练习册系列答案
相关题目
+
=1，P为椭圆在第一象限内的点，它与两焦点的连线互相垂直，求P点的坐标.
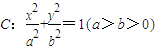经过点P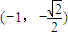
，两焦点为F1、F2，短轴的一个端点为D，且
．
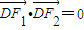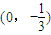，且交椭圆C于A、B两点，证明：以AB为直径的圆恒过定点T（0，1）．
，点P（
）在椭圆上．