题目内容
已知椭圆
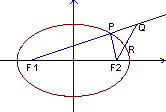
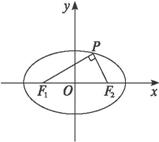
思路解析:设P点的坐标,列方程组解得坐标. 解法一:设P(x0,y0)(x0>0,y0>0),椭圆的两焦点分别是F1(-5,0)、F2(5,0),如图所示,则 ∴ 解方程组,得x0=3,y0=4. ∴P(3,4). 解法二:设P(x0,y0)(x0>0,y0>0), 则有a=3 ∴|PF1|=a+ex0=3 ∵PF1⊥PF2,∴|PF1|2+|PF2|2=|F1F2|2. ∴(3 解得x0=±3. ∵x0>0,y0>0,∴x0=3,y0=4.∴P(3,4). 方法归纳 当已知两直线互相垂直时,常想到其斜率之积为-1;当已知椭圆上一点P时,常想到点P的坐标是椭圆方程的一组解.椭圆上的点与焦点连线,常联想焦半径公式.
![]() ·
·![]() =-1.
=-1.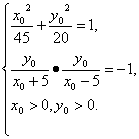
![]() ,b=2
,b=2![]() ,∴c=5,e=
,∴c=5,e=![]() .
.![]() +
+![]() x0,|PF2|=a-ex0=3
x0,|PF2|=a-ex0=3![]() -
-![]() x0,|F1F2|=2c=10.
x0,|F1F2|=2c=10.![]() +
+![]() x0)2+(3
x0)2+(3![]() -
-![]() x0)2=100.
x0)2=100.
 练习册系列答案
练习册系列答案
快乐成长导学案系列答案
快乐练习课时全能练系列答案
课后练习与评价单元测试卷系列答案
学习之友系列答案
学生活动手册系列答案
每周最佳方案系列答案
名校1号系列答案
学习辅导报系列答案
全优考评一卷通系列答案
课外作业系列答案
相关题目