题目内容
已知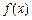 是定义在 [ – 1,1 ] 上的奇函数,且
是定义在 [ – 1,1 ] 上的奇函数,且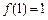 ,若m,
,若m,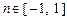 ,
,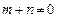 时有
时有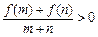 .
.
(1)用定义证明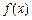 在 [ – 1,1 ] 上是增函数;
在 [ – 1,1 ] 上是增函数;
(2)若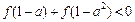 成立,求a的取值范围.
成立,求a的取值范围.
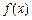 是定义在 [ – 1,1 ] 上的奇函数,且
是定义在 [ – 1,1 ] 上的奇函数,且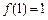 ,若m,
,若m,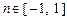 ,
,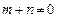 时有
时有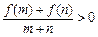 .
.(1)用定义证明
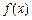 在 [ – 1,1 ] 上是增函数;
在 [ – 1,1 ] 上是增函数;(2)若
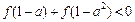 成立,求a的取值范围.
成立,求a的取值范围.(1)见解析(2)

(1) 得 ∴
∴
由题意得:
∵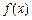 为奇函数
为奇函数
∴
又 ∴
∴
∴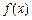 在 [ – 1,1 ] 上是增函数
在 [ – 1,1 ] 上是增函数
(2)
 解得
解得
 ∴
∴
由题意得:

∵
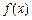 为奇函数
为奇函数∴

又
 ∴
∴
∴
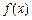 在 [ – 1,1 ] 上是增函数
在 [ – 1,1 ] 上是增函数(2)

 解得
解得

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案
相关题目
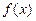 是定义在
是定义在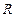 上的单调奇函数, 且
上的单调奇函数, 且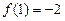 .
.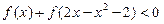 .
.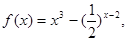 则其零点所在的区间为 ( )
则其零点所在的区间为 ( ) ,已知实数x,y满足|x|≤2,|y|≤2,
,已知实数x,y满足|x|≤2,|y|≤2,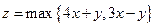 则z的取值范围是 ( )
则z的取值范围是 ( )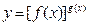 在求导时,可运用对数法:在函数解析式两边求对数得
在求导时,可运用对数法:在函数解析式两边求对数得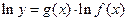 ,两边同时求导得
,两边同时求导得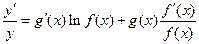 ,于是
,于是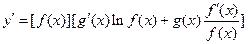 .运用此方法可以探求
.运用此方法可以探求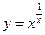 的一个单调递增区间是( )
的一个单调递增区间是( )
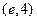
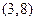

 ,函数
,函数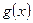 的图像与函数
的图像与函数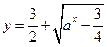
 对称.
对称. 上的值域为
上的值域为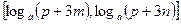 ,
, 的取值范围;
的取值范围;
 .
. 满足对任意的
满足对任意的 都有
都有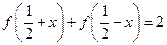 成立,则
成立,则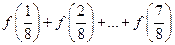 = .
= . 和
和 的图象在
的图象在 处的切线互相平行.
处的切线互相平行. 的值;
的值; ,当
,当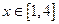 时,
时, 恒成立,求
恒成立,求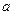 的取值范围.
的取值范围.