题目内容
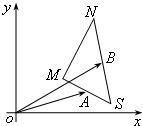
如图，已知| OA |
| e |
| OB |
| e |
| OC |
2
+
| e1 |
| e2 |
2
+
，| e1 |
| e2 |
| OD |
| e1 |
| e2 |
| e1 |
| e2 |
分析：根据向量的线性表示先用基底
、
表示
、
，再化简即可
| OA |
| OB |
| OC |
| OD |
解答：解：
=
+
=
+
=
+
（
-
）=
+
=
×3
+
×3
=2
+
=
+
=
+
=
+
（
-
）=
+
=
× 3
+
×3
=
+2
故答案为：2
+
，
+2
| OC |
| OA |
| AC |
| OA |
| 1 |
| 3 |
| AB |
| OA |
| 1 |
| 3 |
| OB |
| OA |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
| 2 |
| 3 |
| e1 |
| 1 |
| 3 |
| e2 |
| e1 |
| e2 |
| OD |
| OA |
| AD |
| OA |
| 2 |
| 3 |
| AB |
| OA |
| 2 |
| 3 |
| OB |
| OA |
| 1 |
| 3 |
| OA |
| 2 |
| 3 |
| OB |
| 1 |
| 3 |
| e1 |
| 2 |
| 3 |
| e2 |
| e1 |
| e2 |
故答案为：2
| e1 |
| e2 |
| e1 |
| e2 |
点评：本题考查向量的线性表示和加减运算，要求能根据向量的线性表示熟练地将一个向量拆分成两个共起点的向量的差．属简单题
练习册系列答案
相关题目
如图，已知
如图，已知
如图，已知
（2013•潮州二模）如图，已知OA=OB=OC，∠ACB=45°，则∠OBA的大小为