题目内容
若对任意x∈[-1,1],不等式2tx+t2-3<0恒成立,则实数t的取值范围是______________.
(-1,1)
解:令f(x)=2tx+t2-3,则x∈[-1,1]时2tx+t2-3<0恒成立的条件是![]()
即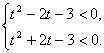
解不等式组得-1<t<1,
∴t的取值范围是(-1,1).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
若对任意x∈[-1,1],不等式2tx+t2-3<0恒成立,则实数t的取值范围是______________.
(-1,1)
解:令f(x)=2tx+t2-3,则x∈[-1,1]时2tx+t2-3<0恒成立的条件是![]()
即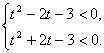
解不等式组得-1<t<1,
∴t的取值范围是(-1,1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案