题目内容
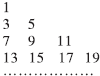 数列an=2n-1(n∈N*)排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
数列an=2n-1(n∈N*)排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )| A、61 | B、62 | C、63 | D、64 |
分析:由三角形数阵分析得到数阵的第n+1行第1列的数在数列{2n-1}中所在的项,验证可知第45行第1列是数列{2n-1}的第991项,而2013是数列{2n-1}的第1007项,由此可推得2013位于数阵中的行与列,从而得到答案.
解答:解:由三角形数阵可知,三角形数阵第n+1行第1列为数列{2n-1}的第
+1项,
第45行第1列为第991项,2013为数列的第1007项,
∴s=45,t=17.
s+t=62.
故选:B.
| n(n+1) |
| 2 |
第45行第1列为第991项,2013为数列的第1007项,
∴s=45,t=17.
s+t=62.
故选:B.
点评:本题考查了等差数列的通项公式,解答的关键是明确所给三角形数阵的特点,求出数阵的第n+1行第1列的数在数列{2n-1}中所在的项,是中低档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
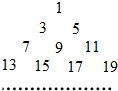 (2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是
(2011•潍坊二模)已知数列an=2n-1(n∈N*),把数列{an}的各项排成如图所示的三角形数阵,记(m,n)表示该数阵中第m行中从左到右的第n个数,则S(10,6)对应于数阵中的数是