题目内容
(本小题满分14分)已知函数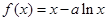 ,
,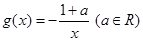 .
.
(Ⅰ)若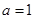 ,求函数
,求函数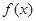 的极值;
的极值;
(Ⅱ)设函数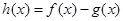 ,求函数
,求函数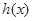 的单调区间;
的单调区间;
(Ⅲ)若在区间 上不存在
上不存在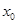 ,使得
,使得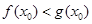 成立,求实数
成立,求实数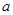 的取值范围.
的取值范围.
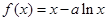 ,
,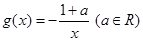 .
.(Ⅰ)若
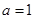 ,求函数
,求函数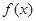 的极值;
的极值;(Ⅱ)设函数
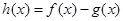 ,求函数
,求函数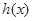 的单调区间;
的单调区间;(Ⅲ)若在区间
 上不存在
上不存在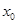 ,使得
,使得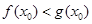 成立,求实数
成立,求实数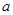 的取值范围.
的取值范围.(Ⅰ)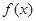 的极小值为
的极小值为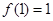 (Ⅱ)
(Ⅱ)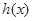 在
在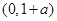 上递减,在
上递减,在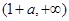 上递增
上递增
(Ⅲ)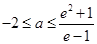
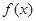 的极小值为
的极小值为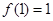 (Ⅱ)
(Ⅱ)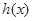 在
在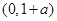 上递减,在
上递减,在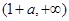 上递增
上递增(Ⅲ)
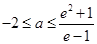
试题分析:(Ⅰ)
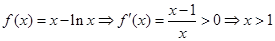 ,
,∴
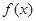 在
在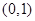 上递减,在
上递减,在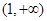 上递增,
上递增,∴
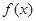 的极小值为
的极小值为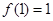 . ……4分
. ……4分(Ⅱ)
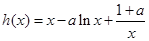 , ∴
, ∴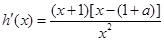 ,
,①当
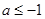 时,
时, ,∴
,∴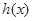 在
在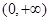 上递增
上递增 ②当
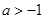 时,
时,
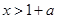 ,
,∴
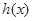 在
在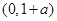 上递减,在
上递减,在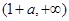 上递增. ……8分
上递增. ……8分(Ⅲ)先解区间
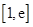 上存在一点
上存在一点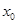 ,使得
,使得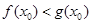 成立
成立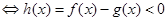 在
在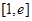 上有解
上有解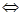 当
当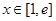 时,
时,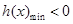 ,
,由(Ⅱ)知
①当
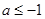 时,
时,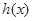 在
在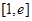 上递增,∴
上递增,∴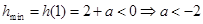 , ∴
, ∴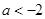 , ……10分
, ……10分②当
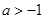 时,
时,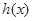 在
在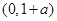 上递减,在
上递减,在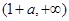 上递增,
上递增,(ⅰ)当
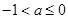 时,
时, 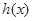 在
在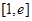 上递增 ∴
上递增 ∴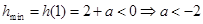 ,∴
,∴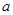 无解,
无解,(ⅱ)当
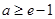 时,
时, 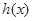 在
在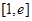 上递减,
上递减, ∴
 , ∴
, ∴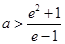 ;
;(ⅲ)当
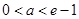 时,
时, 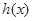 在
在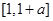 上递减,在
上递减,在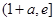 上递增,
上递增,∴
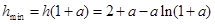 ,
,令
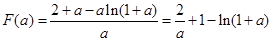 ,则
,则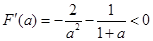 ,
,∴
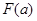 在
在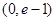 递减, ∴
递减, ∴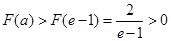 ,∴
,∴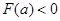 无解,
无解,即
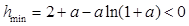 无解
无解 综上可得:存在一点
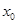 ,使得
,使得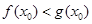 成立,实数
成立,实数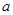 的取值范围为:
的取值范围为: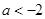 或
或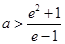 .
.所以不存在一点
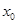 ,使得
,使得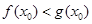 成立,实数
成立,实数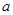 的取值范围为
的取值范围为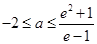 . ……14分
. ……14分点评:导数是研究函数性质的重要工具,研究函数的极值、最值及单调区间时常常用到导数,而求参数的取值范围时,常常需要转化为求最值然后利用导数解决.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
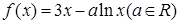 ,
,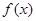 的单调区间和极值点;
的单调区间和极值点; ,记过点
,记过点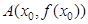 与原点的直线斜率为
与原点的直线斜率为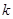 。是否存在
。是否存在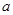 使
使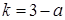 ?若存在,求出
?若存在,求出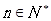 ,曲线
,曲线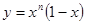 在
在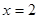 处的切线与
处的切线与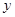 轴的交点的纵坐标为
轴的交点的纵坐标为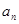 ,则
,则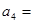 ( )
( )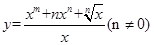
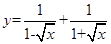
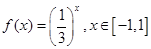 ,函数
,函数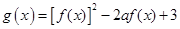 的最小值为
的最小值为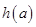 ,
,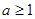 时,求
时,求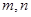 同时满足下列条件:①
同时满足下列条件:①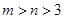 ;②当
;②当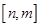 时,值域为
时,值域为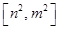
 ?若存在,求出
?若存在,求出 .
.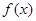 在
在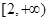 上是增函数,求实数
上是增函数,求实数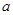 的取值范围;
的取值范围;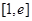 上的最小值为3,求实数
上的最小值为3,求实数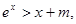 恒成立,则m的取值范围是 。
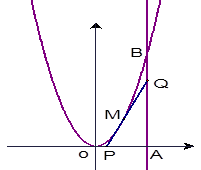
恒成立,则m的取值范围是 。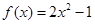 的图像上一点
的图像上一点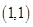 及邻近一点
及邻近一点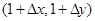 ,则
,则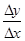 和
和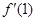 分别等于( )
分别等于( )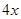 ,4
,4 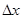 ,4
,4 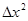 ,3
,3